题目内容
7．下列说法：①a为任意有理数，a2+1总是正数；②如果a+|a|=0，则a＜0；③两点确定一条直线；④若MA=MB，则点M是线段AB的中点．其中正确的有（ ）| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
分析 根据非负数的性质对①进行判断；根据绝对值的意义对②进行判断；根据直线公理对③进行判断；根据线段中点的定义对④进行判断．
解答 解：a为任意有理数，a2+1总是正数，所以①正确；
如果a+|a|=0，则a≤0，所以②错误；
两点确定一条直线，所以③正确；
若MA=MB且M点在线段AB上，则点M是线段AB的中点，所以④错误．
故选C．
点评 本题考查了两点间的距离：连接两点间的线段的长度叫两点间的距离．也考查了非负数的性质．
练习册系列答案
培优好卷单元加期末卷系列答案
一线名师权威作业本系列答案
相关题目
如图所示，若AB∥CD，则∠1，∠2，∠3之间的关系是：∠1=∠2+∠3．
15．
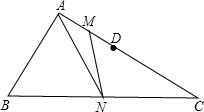如图，在△ABC中，∠BAC=90°，点D在边AC上，AB=CD，点M、N分别为AD、BC的中点，连接MN、AN，MN=3$\sqrt{2}$，AD=4，则线段AN的长为$\sqrt{34}$．
如图，在△ABC中，∠BAC=90°，点D在边AC上，AB=CD，点M、N分别为AD、BC的中点，连接MN、AN，MN=3$\sqrt{2}$，AD=4，则线段AN的长为$\sqrt{34}$． 
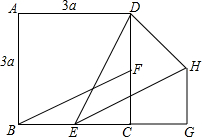如图，正方形ABCD的边长为3a，两动点E、F分别从顶点B、C同时开始以相同速度沿BC、CD运动，与△BCF相应的△EGH在运动过程中始终保持△EGH≌△BCF，B、E、C、G在一直线上，△DHE的面积的最小值是$\frac{27}{8}$a2．
19．在一个不透明的口袋中装有颜色不同的1个蓝球，2个白球，3个红球，4个黄球，从中任意摸出1个红球的概率是（ ）
| A． | $\frac{1}{10}$ | B． | $\frac{3}{10}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |
