题目内容
17.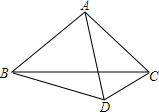 如图,△ABC是等边三角形,点D是△ABC外一点,试证明:DB+DC≥AD.
如图,△ABC是等边三角形,点D是△ABC外一点,试证明:DB+DC≥AD.
分析 将△BCD绕点C顺时针旋转60°得到△CAM,连接AM,则AM=DB,CM=DC,∠DCM=60°,得出△DCM是等边三角形,因此DM=CD=CM,由三角形的三边关系即可得出结论.
解答 证明:将△BCD绕点C顺时针旋转60°得到△CAM,连接AM,如图所示:
则AM=DB,CM=DC,∠DCM=60°,
∴△DCM是等边三角形,
∴DM=CD=CM,
∴AM+DM≥AD(当M在AD上时等号成立),
∴DB+DC≥AD.
点评 本题考查了旋转的性质、等边三角形的性质与判定、三角形的三边关系等知识;熟练掌握旋转的性质,证明△DCM是等边三角形是解决问题的关键.

练习册系列答案
相关题目
18. 如图,AB∥EF∥CD,AD∥MN∥BC,则图中共有平行四边形( )
如图,AB∥EF∥CD,AD∥MN∥BC,则图中共有平行四边形( )
 如图,AB∥EF∥CD,AD∥MN∥BC,则图中共有平行四边形( )
如图,AB∥EF∥CD,AD∥MN∥BC,则图中共有平行四边形( )| A. | 6个 | B. | 7个 | C. | 8个 | D. | 9个 |
9.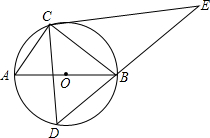 如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=10,AC=6,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )
如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=10,AC=6,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )
 如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=10,AC=6,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )
如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=10,AC=6,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )| A. | $\frac{20}{3}$ | B. | $\frac{40}{3}$ | C. | 16 | D. | $\frac{64}{5}$ |
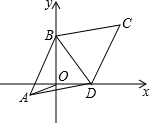 如图,已知平行四边形ABCD中,AB=BC,BC=10,∠BCD=60°,两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接OA,则OA的长的最小值是5$\sqrt{3}$-5.
如图,已知平行四边形ABCD中,AB=BC,BC=10,∠BCD=60°,两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接OA,则OA的长的最小值是5$\sqrt{3}$-5. 已知CA=CB,CD=CE,B、C、E在同一条直线上,∠BCA=∠DCE=60°.
已知CA=CB,CD=CE,B、C、E在同一条直线上,∠BCA=∠DCE=60°.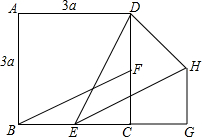 如图,正方形ABCD的边长为3a,两动点E、F分别从顶点B、C同时开始以相同速度沿BC、CD运动,与△BCF相应的△EGH在运动过程中始终保持△EGH≌△BCF,B、E、C、G在一直线上,△DHE的面积的最小值是$\frac{27}{8}$a2.
如图,正方形ABCD的边长为3a,两动点E、F分别从顶点B、C同时开始以相同速度沿BC、CD运动,与△BCF相应的△EGH在运动过程中始终保持△EGH≌△BCF,B、E、C、G在一直线上,△DHE的面积的最小值是$\frac{27}{8}$a2.