题目内容
10.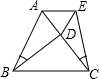 已知,如图△ABC为等边三角形,且∠ACE=∠ABD,CE=BD,试说明:
已知,如图△ABC为等边三角形,且∠ACE=∠ABD,CE=BD,试说明:(1)△ADE是等边三角形;
(2)CD+DE=AB.
分析 (1)只要证明△ABD≌△ACE,得AD=AE,∠BAD=∠CAE=60°,由此即可证明.
(2)由(1)可知AD=ED,CD+DE=CD+AD=AC,由此即可证明.
解答 (1)证明:∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
在△ABD和△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠ABD=∠ACE}\\{BD=CE}\end{array}\right.$,
∴△ABD≌△ACE,
∴AD=AE,∠BAD=∠CAE=60°,
∴△ADE是等边三角形.
(2)∵△ADE是等边三角形,
∴DE=AD,
∴CD+DE=CD+AD=AC=AB.
点评 本题考查全等三角形的判定和性质、等边三角形的判定和性质,解题关键是正确寻找全等三角形,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.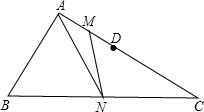 如图,在△ABC中,∠BAC=90°,点D在边AC上,AB=CD,点M、N分别为AD、BC的中点,连接MN、AN,MN=3$\sqrt{2}$,AD=4,则线段AN的长为$\sqrt{34}$.
如图,在△ABC中,∠BAC=90°,点D在边AC上,AB=CD,点M、N分别为AD、BC的中点,连接MN、AN,MN=3$\sqrt{2}$,AD=4,则线段AN的长为$\sqrt{34}$.
 如图,在△ABC中,∠BAC=90°,点D在边AC上,AB=CD,点M、N分别为AD、BC的中点,连接MN、AN,MN=3$\sqrt{2}$,AD=4,则线段AN的长为$\sqrt{34}$.
如图,在△ABC中,∠BAC=90°,点D在边AC上,AB=CD,点M、N分别为AD、BC的中点,连接MN、AN,MN=3$\sqrt{2}$,AD=4,则线段AN的长为$\sqrt{34}$.
19.在一个不透明的口袋中装有颜色不同的1个蓝球,2个白球,3个红球,4个黄球,从中任意摸出1个红球的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
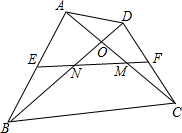 在四边形ABCD中,ACBD相交于O点,AC=BD,E、F分别是AB,CD的中点,连接EF分别交AC、BD于M、N,判断三角形MON的形状,并说明理由.
在四边形ABCD中,ACBD相交于O点,AC=BD,E、F分别是AB,CD的中点,连接EF分别交AC、BD于M、N,判断三角形MON的形状,并说明理由.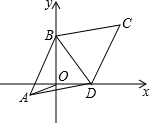 如图,已知平行四边形ABCD中,AB=BC,BC=10,∠BCD=60°,两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接OA,则OA的长的最小值是5$\sqrt{3}$-5.
如图,已知平行四边形ABCD中,AB=BC,BC=10,∠BCD=60°,两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接OA,则OA的长的最小值是5$\sqrt{3}$-5.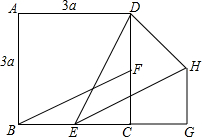 如图,正方形ABCD的边长为3a,两动点E、F分别从顶点B、C同时开始以相同速度沿BC、CD运动,与△BCF相应的△EGH在运动过程中始终保持△EGH≌△BCF,B、E、C、G在一直线上,△DHE的面积的最小值是$\frac{27}{8}$a2.
如图,正方形ABCD的边长为3a,两动点E、F分别从顶点B、C同时开始以相同速度沿BC、CD运动,与△BCF相应的△EGH在运动过程中始终保持△EGH≌△BCF,B、E、C、G在一直线上,△DHE的面积的最小值是$\frac{27}{8}$a2.