题目内容
10.下列关于因式分解的情况正确的是( )| A. | 4x2y+xy+3xy2=xy(4x+3y) | B. | $\frac{1}{4}$a2+ab+b2=$\frac{1}{4}$(a+2b)2 | ||
| C. | m2+4=(m+2)2 | D. | 若x2-x+42=(x+a)(x+b),则a,b异号 |
分析 直接利用提取公因式法以及公式法分解因式得出答案.
解答 解:A、4x2y+xy+3xy2=xy(4x+3y+1),故此选项错误;
B、$\frac{1}{4}$a2+ab+b2=($\frac{1}{2}$a+b)2,故此选项错误;
C、m2+4无法分解因式,故此选项错误;
D、若x2-x+42=(x+a)(x+b)=(a+6)(x-7),则a,b异号,正确.
故选:D.
点评 此题主要考查了提取公因式法以及公式法分解因式,正确分解因式是解题关键.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
11. 将一把直尺与一块三角板如图放置,若∠1=46°,则∠2的度数为( )
将一把直尺与一块三角板如图放置,若∠1=46°,则∠2的度数为( )
 将一把直尺与一块三角板如图放置,若∠1=46°,则∠2的度数为( )
将一把直尺与一块三角板如图放置,若∠1=46°,则∠2的度数为( )| A. | 136° | B. | 138° | C. | 140° | D. | 142° |
18.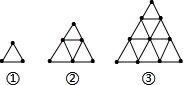 探索规律并填空
探索规律并填空
1+2=$\frac{2×(1+2)}{2}$;
1+2+3=$\frac{3×(1+3)}{2}$;
1+2+3+4=$\frac{4×(1+4)}{2}$;
1+2+3…+20=210;
1+2+3+…+n=$\frac{n(n+1)}{2}$.
用火柴棒按下面的方式搭图形填写表
照规律搭下去:
(1)第n个图形的大三角形周长的火柴棒是几根?
(2)第n个图形的小三角形个数有几个?第200个图形的小三角形个数有几个?
 探索规律并填空
探索规律并填空1+2=$\frac{2×(1+2)}{2}$;
1+2+3=$\frac{3×(1+3)}{2}$;
1+2+3+4=$\frac{4×(1+4)}{2}$;
1+2+3…+20=210;
1+2+3+…+n=$\frac{n(n+1)}{2}$.
用火柴棒按下面的方式搭图形填写表
| 图形编号 | ① | ② | ③ | ④ |
| 大三角形周长的火柴棒根数 | 3 | 6 | 9 | 12 |
| 小三角形个数 | 1 | 4 | 9 | 16 |
(1)第n个图形的大三角形周长的火柴棒是几根?
(2)第n个图形的小三角形个数有几个?第200个图形的小三角形个数有几个?
2.下列图形中,∠1和∠2是内错角的是( )
| A. | 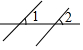 | B. | 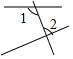 | C. | 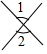 | D. | 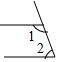 |
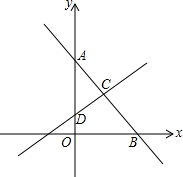 如图,直线AB分别与y轴,x轴交于点A(0,4)和点B(3,0),直线CD垂直平分线段AB交AB于点C,交y轴于点D.
如图,直线AB分别与y轴,x轴交于点A(0,4)和点B(3,0),直线CD垂直平分线段AB交AB于点C,交y轴于点D.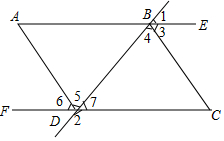 如图,已知∠1+∠2=180°,∠A=∠C,AD平分∠FDB,试问∠3与∠4有怎样的数量关系,并说明理由.
如图,已知∠1+∠2=180°,∠A=∠C,AD平分∠FDB,试问∠3与∠4有怎样的数量关系,并说明理由.