题目内容
19．分解因式：18b（a-b）2-12（a-b）3=6（a-b）2（5b-2a）．分析 根据提公因式法，可得答案．
解答 解：原式=6（a-b）2[3b-2（a-b）]
=6（a-b）2（5b-2a），
故答案为：6（a-b）2（5b-2a）．
点评 本题考查了因式分解，确定公因式是解题关键．
练习册系列答案
相关题目
20．下列运算正确的是（ ）
| A． | a3•a4=a7 | B． | （3a-b）2=9a2-b2 | C． | （ab）3=ab3 | D． | 4a-3a=1 |
10．下列关于因式分解的情况正确的是（ ）
| A． | 4x2y+xy+3xy2=xy（4x+3y） | B． | $\frac{1}{4}$a2+ab+b2=$\frac{1}{4}$（a+2b）2 | ||
| C． | m2+4=（m+2）2 | D． | 若x2-x+42=（x+a）（x+b），则a，b异号 |
7．下列说法正确的是（ ）
| A． | （-3）2的算术平方根是3 | B． | $\sqrt{225}$的平方根是±15 | ||
| C． | 当x=0或2时，x$\sqrt{x-2}$=0 | D． | $\frac{\sqrt{3}}{2}$是分数 |
14．已知2：x=3：9，则x=（ ）
| A． | 2 | B． | 3 | C． | 4 | D． | 6 |
11．
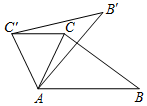如图，在△ABC中，∠CAB=65°，在同一平面内，将△ABC绕点A按逆时针方向旋转到△AB'C'的位置，使得CC'∥AB，则∠BAB'=（ ）
如图，在△ABC中，∠CAB=65°，在同一平面内，将△ABC绕点A按逆时针方向旋转到△AB'C'的位置，使得CC'∥AB，则∠BAB'=（ ）| A． | 30° | B． | 35° | C． | 40° | D． | 50° |
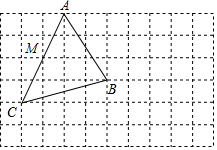如图，在边长为1的正方形网格中有△ABC，请按下列要求画图并解答问题．