题目内容
20.解下列方程组:(1)$\left\{\begin{array}{l}2x+y=2\\ 3x-2y=10\end{array}\right.$
(2)$\left\{\begin{array}{l}3({x+y})-4({x-y})=4\\ \frac{x+y}{2}+\frac{x-y}{6}=1\end{array}\right.$.
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{2x+y=2①}\\{3x-2y=10②}\end{array}\right.$,
①×2+②得:7x=14,
解得:x=2,
把x=2代入①得:y=-2,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-2}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{-x+7y=4①}\\{2x+y=3②}\end{array}\right.$,
①×2+②得:15y=11,
解得:y=$\frac{11}{15}$,
把y=$\frac{11}{15}$代入①得:x=$\frac{17}{15}$,
则方程组的解为$\left\{\begin{array}{l}{x=\frac{17}{15}}\\{y=\frac{11}{15}}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
10.下列关于因式分解的情况正确的是( )
| A. | 4x2y+xy+3xy2=xy(4x+3y) | B. | $\frac{1}{4}$a2+ab+b2=$\frac{1}{4}$(a+2b)2 | ||
| C. | m2+4=(m+2)2 | D. | 若x2-x+42=(x+a)(x+b),则a,b异号 |
11.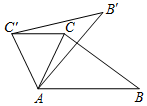 如图,在△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A按逆时针方向旋转到△AB'C'的位置,使得CC'∥AB,则∠BAB'=( )
如图,在△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A按逆时针方向旋转到△AB'C'的位置,使得CC'∥AB,则∠BAB'=( )
 如图,在△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A按逆时针方向旋转到△AB'C'的位置,使得CC'∥AB,则∠BAB'=( )
如图,在△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A按逆时针方向旋转到△AB'C'的位置,使得CC'∥AB,则∠BAB'=( )| A. | 30° | B. | 35° | C. | 40° | D. | 50° |
15.下列结论正确的是( )
| A. | 不相交的两条直线叫做平行线 | |
| B. | 两条直线被第三条直线所截,同位角相等 | |
| C. | 垂直于同一条直线的两条直线互相平行 | |
| D. | 平行于同一条直线的两条直线互相平行 |
5.下列调查中,最适合采用普查方式的是( )
| A. | 调查2017年春节晚会的收视率 | |
| B. | 调查宝应湖中鱼的种类和数量 | |
| C. | 调查某品牌节能灯的使用寿命 | |
| D. | 调查某航班的旅客是否携带了违禁物品 |
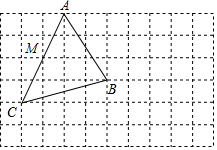 如图,在边长为1的正方形网格中有△ABC,请按下列要求画图并解答问题.
如图,在边长为1的正方形网格中有△ABC,请按下列要求画图并解答问题. 观察下列图案,在A、B、C、D四幅图案中,能通过图案(1)平移得到的是( )
观察下列图案,在A、B、C、D四幅图案中,能通过图案(1)平移得到的是( )


