题目内容
1.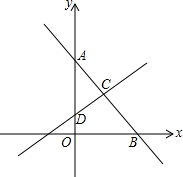 如图,直线AB分别与y轴,x轴交于点A(0,4)和点B(3,0),直线CD垂直平分线段AB交AB于点C,交y轴于点D.
如图,直线AB分别与y轴,x轴交于点A(0,4)和点B(3,0),直线CD垂直平分线段AB交AB于点C,交y轴于点D.(1)求点D的坐标;
(2)求直线CD的解忻式.
分析 (1)设点D坐标为(0,m),由中垂线的性质得DA=DB,利用两点间的距离公式列出关于m的方程,解之可得答案;
(2)先利用中点的坐标公式求得点C的坐标,再利用待定系数法求直线CD的解析式.
解答 解:(1)设点D坐标为(0,m),
∵CD垂直且平分AB,
∴DA=DB,
∵A(0,4)、B(3,0),
∴$\sqrt{(0-0)^{2}+(4-m)^{2}}$=$\sqrt{(3-0)^{2}+(0-m)^{2}}$,
解得:m=$\frac{7}{8}$,
∴点D的坐标为(0,$\frac{7}{8}$);
(2)∵A(0,4)、B(3,0),且C为AB的中点,
∴点C的坐标为($\frac{0+3}{2}$,$\frac{0+4}{2}$),即($\frac{3}{2}$,2),
设直线CD的解析式为y=kx+b,
把D(0,$\frac{7}{8}$),C($\frac{3}{2}$,2)代入,得:
$\left\{\begin{array}{l}{b=\frac{7}{8}}\\{\frac{3}{2}k+b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=\frac{7}{8}}\end{array}\right.$.
故直线CD的解析式为y=$\frac{3}{4}$x+$\frac{7}{8}$.
点评 本题考查了两直线相交或平行问题,熟练掌握两点间的距离公式、线段的中点坐标的公式及待定系数法求直线的解析式是解题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
20.下列运算正确的是( )
| A. | a3•a4=a7 | B. | (3a-b)2=9a2-b2 | C. | (ab)3=ab3 | D. | 4a-3a=1 |
10.下列关于因式分解的情况正确的是( )
| A. | 4x2y+xy+3xy2=xy(4x+3y) | B. | $\frac{1}{4}$a2+ab+b2=$\frac{1}{4}$(a+2b)2 | ||
| C. | m2+4=(m+2)2 | D. | 若x2-x+42=(x+a)(x+b),则a,b异号 |
11.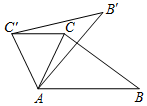 如图,在△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A按逆时针方向旋转到△AB'C'的位置,使得CC'∥AB,则∠BAB'=( )
如图,在△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A按逆时针方向旋转到△AB'C'的位置,使得CC'∥AB,则∠BAB'=( )
 如图,在△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A按逆时针方向旋转到△AB'C'的位置,使得CC'∥AB,则∠BAB'=( )
如图,在△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A按逆时针方向旋转到△AB'C'的位置,使得CC'∥AB,则∠BAB'=( )| A. | 30° | B. | 35° | C. | 40° | D. | 50° |
 如图,一大桥的桥拱为抛物线形,跨度AB=50米,拱高(即顶点C到AB的距离)为20米,求桥拱所在抛物线的表达式.
如图,一大桥的桥拱为抛物线形,跨度AB=50米,拱高(即顶点C到AB的距离)为20米,求桥拱所在抛物线的表达式. 如图,在△ABC中,AB=AC,∠ABC的平分线与△ABC的外角平分线相交于点D,若∠BDC=25°,则∠ABC的度数为65°.
如图,在△ABC中,AB=AC,∠ABC的平分线与△ABC的外角平分线相交于点D,若∠BDC=25°,则∠ABC的度数为65°.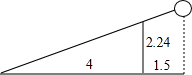 已知女排赛场标准球网的高度是2.24米,在2016年奥运会女排比赛中,某队球员在一次扣球时,球恰好擦网而过(击球擦网落地过程为直线),落在对方场地距离球网4米的位置上,此时该运动员距离球网1.5米,则该运动员击球的高度是3.08米.
已知女排赛场标准球网的高度是2.24米,在2016年奥运会女排比赛中,某队球员在一次扣球时,球恰好擦网而过(击球擦网落地过程为直线),落在对方场地距离球网4米的位置上,此时该运动员距离球网1.5米,则该运动员击球的高度是3.08米.