题目内容
11.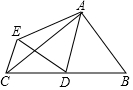 如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE,则线段CE的长等于( )
如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE,则线段CE的长等于( )| A. | 2 | B. | $\frac{5}{4}$ | C. | $\frac{5}{3}$ | D. | $\frac{7}{5}$ |
分析 如图连接BE交AD于O,作AH⊥BC于H.首先证明AD垂直平分线段BE,△BCE是直角三角形,求出BC、BE,在Rt△BCE中,利用勾股定理即可解决问题.
解答 解: 如图连接BE交AD于O,作AH⊥BC于H.
如图连接BE交AD于O,作AH⊥BC于H.
在Rt△ABC中,∵AC=4,AB=3,
∴BC=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵CD=DB,
∴AD=DC=DB=$\frac{5}{2}$,
∵$\frac{1}{2}$•BC•AH=$\frac{1}{2}$•AB•AC,
∴AH=$\frac{12}{5}$,
∵AE=AB,DE=DB=DC,
∴AD垂直平分线段BE,△BCE是直角三角形,
∵$\frac{1}{2}$•AD•BO=$\frac{1}{2}$•BD•AH,
∴OB=$\frac{12}{5}$,
∴BE=2OB=$\frac{24}{5}$,
在Rt△BCE中,EC=$\sqrt{B{C}^{2}-B{E}^{2}}$=$\sqrt{{5}^{2}-(\frac{24}{5})^{2}}$=$\frac{7}{5}$,
故选D.
点评 本题考查翻折变换、直角三角形的斜边中线的性质、勾股定理等知识,解题的关键是学会利用面积法求高,属于中考常考题型.

练习册系列答案
相关题目
2. 如图是某个几何体的主视图、左视图、俯视图,该几何体是( )
如图是某个几何体的主视图、左视图、俯视图,该几何体是( )
 如图是某个几何体的主视图、左视图、俯视图,该几何体是( )
如图是某个几何体的主视图、左视图、俯视图,该几何体是( )| A. | 圆柱 | B. | 球 | C. | 圆锥 | D. | 棱锥 |
6. 如图,在△ABC中,∠BAC=x,∠B=2x,∠C=3x,则∠BAD=( )
如图,在△ABC中,∠BAC=x,∠B=2x,∠C=3x,则∠BAD=( )
 如图,在△ABC中,∠BAC=x,∠B=2x,∠C=3x,则∠BAD=( )
如图,在△ABC中,∠BAC=x,∠B=2x,∠C=3x,则∠BAD=( )| A. | 145° | B. | 150° | C. | 155° | D. | 160° |
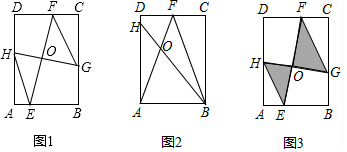
 如图,在?ABCD中,点E、F分别在AD、BC上,且AE=CF,EF、BD相交于点O,求证:OE=OF.
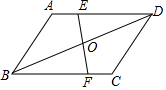
如图,在?ABCD中,点E、F分别在AD、BC上,且AE=CF,EF、BD相交于点O,求证:OE=OF. 如图,四边形ABCD与四边形EFGH位似,位似中心点是O,$\frac{OE}{OA}$=$\frac{3}{5}$,则$\frac{FG}{BC}$=$\frac{3}{5}$.
如图,四边形ABCD与四边形EFGH位似,位似中心点是O,$\frac{OE}{OA}$=$\frac{3}{5}$,则$\frac{FG}{BC}$=$\frac{3}{5}$.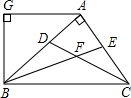 如图,AB⊥AC,AG⊥BG,CD、BE分别是∠ACB,∠ABC的角平分线,AG∥BC,下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°、其中正确的结论是( )
如图,AB⊥AC,AG⊥BG,CD、BE分别是∠ACB,∠ABC的角平分线,AG∥BC,下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°、其中正确的结论是( )