题目内容
19.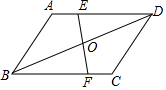 如图,在?ABCD中,点E、F分别在AD、BC上,且AE=CF,EF、BD相交于点O,求证:OE=OF.
如图,在?ABCD中,点E、F分别在AD、BC上,且AE=CF,EF、BD相交于点O,求证:OE=OF.
分析 方法1、连接BE、DF,由已知证出四边形BEDF是平行四边形,即可得出结论.
方法2、先判断出DE=BF,进而判断出△DOE≌△BOF即可.
解答 证明: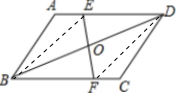 方法1,连接BE、DF,如图所示:
方法1,连接BE、DF,如图所示:
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AE=CF,
∴DE=BF,
∴四边形BEDF是平行四边形,
∴OF=OE.
方法2,∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵∠ODE=∠OBF,AE=CF,
∴DE=BF,
在△DOE和△BOF中,$\left\{\begin{array}{l}{∠DOE=∠BOF}\\{∠ODE=∠OBF}\\{DE=BF}\end{array}\right.$,
∴△DOE≌△BOF(AAS),
∴OE=OF.
点评 本题考查了平行四边形的判定与性质;通过作辅助线证明四边形BEDF是平行四边形是解决问题的关键.

练习册系列答案
相关题目
10. 某运动会颁奖台如图所示,它的主视图是( )
某运动会颁奖台如图所示,它的主视图是( )
 某运动会颁奖台如图所示,它的主视图是( )
某运动会颁奖台如图所示,它的主视图是( )| A. |  | B. |  | ||
| C. |  | D. |  |
11.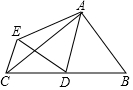 如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE,则线段CE的长等于( )
如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE,则线段CE的长等于( )
 如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE,则线段CE的长等于( )
如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE,则线段CE的长等于( )| A. | 2 | B. | $\frac{5}{4}$ | C. | $\frac{5}{3}$ | D. | $\frac{7}{5}$ |
10.能用平方差公式计算的是( )
| A. | (-x+2y)(x-2y) | B. | (2x-y)(2y+x) | C. | (m-n)(n-m) | D. | 99×101 |
 在“三角尺拼角”实验中,小明同学把一副三角尺按如图所示的方式放置,则∠1=120°.
在“三角尺拼角”实验中,小明同学把一副三角尺按如图所示的方式放置,则∠1=120°.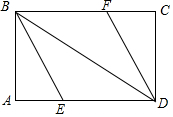 如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.
如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.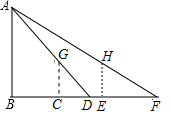 小强为测量一路灯杆AB的高度,在灯光下,小强在C处的影长为3米,沿BC方向行走了5米到E处,此时小强的影长为5米,若小强身高为1.7米,求路灯杆AB的高度.
小强为测量一路灯杆AB的高度,在灯光下,小强在C处的影长为3米,沿BC方向行走了5米到E处,此时小强的影长为5米,若小强身高为1.7米,求路灯杆AB的高度.