题目内容
10.(一)问题:你能比较两个数20102011和20112010的大小吗?为解决这个问题,我们先把它抽象成数学问题,写出它的一般形式,即比较nn+1和(n+1)n的大小(n为自然数),然后从简单情形入手,从中发现规律,经过归纳猜想出结论.
(1)通过计算,比较下列各组数的大小:
①12<21;②23<32;③34>43;④45>54;⑤56>65…
(2)从第(1)题的结果经过归纳,可以猜想出nn+1>(n+1)n(n≥3)
(3)根据上面归纳猜想得到的一般结论,试比较下列两个数的大小:
①20102011>20112010;②-20102011<-20112010
(二)请比较大小:
$\frac{{2}^{2011}+1}{{2}^{2012}+1}$>$\frac{{2}^{2012}+1}{{2}^{2013}+1}$(直接写出猜想结果不必简述理由).
分析 (1)根据有理数的乘方的定义分别进行计算,再进行比较即可;
(2)根据上述得出的答案解答即可;
(3)①根据(2)的结论解答即可,②根据不等式性质,两边同时除以-1,不等号方向不变;
(4)分别通分后,比较分子的大小即可.
解答 解:(1)①12=1,21=2,则12<21;
②23=8,32=9,则23<32;
③34=81,43=64,则34>43;
④45=1024,54=625,则45>54;
⑤56=15625,65=7776,则56>65;
故答案为:<,<,>,>,>;
(2)从上面的结果经过归纳,可以猜想出nn+1和(n+1)n的大小关系是:
当n<3时,nn+1<(n+1)n,
当n≥3时,nn+1>(n+1)n;
故答案为:>;
(3)①∵2010>3,
∴20102011>20112010.
②-20102011<-20112010,
故答案为:>,<;
(4)∵$\frac{{2}^{2011}+1}{{2}^{2012}+1}$=$\frac{({2}^{2011}+1)({2}^{2013}+1)}{({2}^{2012}+1)({2}^{2013}+1)}$=$\frac{{2}^{4024}+{2}^{2011}+{2}^{2013}+1}{({2}^{2012}+1)({2}^{2013}+1)}$,
$\frac{{2}^{2012}+1}{{2}^{2013}+1}$=$\frac{({2}^{2012}+1)^{2}}{({2}^{2012}+1)({2}^{2013}+1)}$,
∵(22012+1)2=24024+2×22012+1=24024+22013+1<24024+22011+22013+1,
∴$\frac{{2}^{2011}+1}{{2}^{2012}+1}$>$\frac{{2}^{2012}+1}{{2}^{2013}+1}$;
故答案为:>.
点评 本题考查了有理数的乘方,有理数的大小比较、不等式的性质,理解有理数的乘方的意义准确计算是解题的关键.

 科学实验活动册系列答案
科学实验活动册系列答案| A. | a≤-l | B. | a≤-2 | C. | a≤1且a≠-2 | D. | a≤-1且a≠-2 |
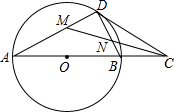 如图,在⊙O中,点D是⊙O上的一点,点C是直径AB延长线上一点,连接BD,CD,且∠A=∠BDC.
如图,在⊙O中,点D是⊙O上的一点,点C是直径AB延长线上一点,连接BD,CD,且∠A=∠BDC.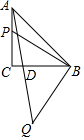 如图,△ABC是等腰直角三角形,∠C=90°,点P是直线AC上一个动点,连结BP,过点B作BQ⊥BP,且使BP=BQ,连结AQ且与直线BC相交于点D.若AP=2,AC=5,则BD的长为4或6.
如图,△ABC是等腰直角三角形,∠C=90°,点P是直线AC上一个动点,连结BP,过点B作BQ⊥BP,且使BP=BQ,连结AQ且与直线BC相交于点D.若AP=2,AC=5,则BD的长为4或6.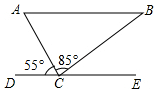 如图,在△ABC中,∠ACB=85°,DE过点C,且DE∥AB,若∠ACD=55°,则∠B的度数是40°.
如图,在△ABC中,∠ACB=85°,DE过点C,且DE∥AB,若∠ACD=55°,则∠B的度数是40°. 如图,在一个高为BC为6m,长AC为10m,宽为2.5m的楼梯表面铺设地毯,若每平方米地毯40元,则铺设地毯至少需要花费1400元钱.
如图,在一个高为BC为6m,长AC为10m,宽为2.5m的楼梯表面铺设地毯,若每平方米地毯40元,则铺设地毯至少需要花费1400元钱.