题目内容
为了从甲、乙两名运动员中选拔一人参加运动会,对他们的10次成绩进行分析,数据如下:
甲:70 80 60 80 60 50 90 100 70 40
乙:90 50 70 80 70 60 80 60 70 70
通过计算确定,应让哪个运动员参加运动会较好?
甲:70 80 60 80 60 50 90 100 70 40
乙:90 50 70 80 70 60 80 60 70 70
通过计算确定,应让哪个运动员参加运动会较好?
考点:方差,算术平均数
专题:
分析:比较甲、乙两人的成绩的方差作出判断.
解答:解:(1)
=
(70+80+60+80+60+50+90+100+70+40)=70;
S甲2=
[(70-70)2+(80-70)2+(60-70)2+(80-70)2+(60-70)2+(50-70)2+(90-70)2+(100-70)2+(70-70)2+(40-70)2]=300;
=
(90+50+70+80+70+60+80+60+70+70)=70;
S乙2=
[(90-70)2+(50-70)2+(70-70)2+(80-70)2+(70-70)2+(60-70)2+(80-70)2+(60-70)2+(70-70)2+(70-70)2]=120;
∴因为甲、乙两名同学10次成绩的平均数相同,乙同学的方差小于甲同学的方差,
∴乙同学的成绩较稳定,应选乙参加比赛.
. |
| x甲 |
| 1 |
| 10 |
S甲2=
| 1 |
| 10 |
. |
| x乙 |
| 1 |
| 10 |
S乙2=
| 1 |
| 10 |
∴因为甲、乙两名同学10次成绩的平均数相同,乙同学的方差小于甲同学的方差,
∴乙同学的成绩较稳定,应选乙参加比赛.
点评:本题考查一组数据的方差的意义,是一个基础题,解题时注意平均数是反映数据的平均水平,而方差反映波动的大小,波动越小数据越稳定.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
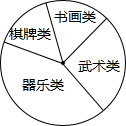 某校学生会准备调查八年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数.
某校学生会准备调查八年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数.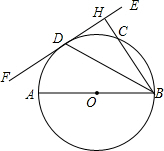 如图,AB为⊙O的直径,EF切⊙O于点D,过点B作BH⊥EF于点H,交⊙O于点C,连接BD.
如图,AB为⊙O的直径,EF切⊙O于点D,过点B作BH⊥EF于点H,交⊙O于点C,连接BD.