题目内容
10.如图,线段AB=10cm,C是线段AB上一点,AC=4cm,M是AB的中点,N是AC的中点.求(1)线段CM的长;(2)求线段MN的长.
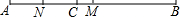
分析 (1)根据M是AB的中点,求出AM,再利用CM=AM-AC求得线段CM的长;
(1)根据N是AC的中点求出NC的长度,再利用MN=CM+NC即可求出MN的长度.
解答 解:(1)由AB=10,M是AB的中点,所以AM=5,
又AC=4,所以CM=AM-AC=5-4=1(cm).
所以线段CM的长为1cm;
(2)因为N是AC的中点,所以NC=2,
所以MN=NC+CM,2+1=3(cm),
所以线段MN的长为3cm.
点评 本题主要考查两点间的距离,线段中点的运用,知道线段的中点把线段分成两条相等的线段是解题的关键.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
15. 如图,把一个长方形纸片沿EF折叠后,点D,C分别落在点D′,C′的位置,若∠EFB=70°,则∠AED′等于( )
如图,把一个长方形纸片沿EF折叠后,点D,C分别落在点D′,C′的位置,若∠EFB=70°,则∠AED′等于( )
 如图,把一个长方形纸片沿EF折叠后,点D,C分别落在点D′,C′的位置,若∠EFB=70°,则∠AED′等于( )
如图,把一个长方形纸片沿EF折叠后,点D,C分别落在点D′,C′的位置,若∠EFB=70°,则∠AED′等于( )| A. | 40° | B. | 50° | C. | 65° | D. | 70° |
2.圆锥的体积是120立方分米,底面积是10平方分米,高是( )分米.
| A. | 12 | B. | 24 | C. | 36 | D. | 48 |
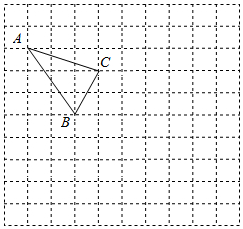 如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点)ABC的顶点A,C的坐标分别为(-4,4),(-1,3).
如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点)ABC的顶点A,C的坐标分别为(-4,4),(-1,3). 尺规作图:
尺规作图: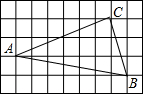 如图,在9×5的正方形网格中,每个小正方形边长均为1,△ABC的顶点均在格点上.
如图,在9×5的正方形网格中,每个小正方形边长均为1,△ABC的顶点均在格点上.