题目内容
10.校园广播主持人培训班开展比赛活动,分为 A、B、C、D四个等级,对应的成绩分别是9分、8分、7分、6分,根据如图不完整的统计图解答下列问题:(1)补全下面两个统计图(不写过程);
(2)求该班学生比赛的平均成绩;
(3)现准备从等级A的4人(两男两女)中随机抽取两名主持人,请利用列表或画树状图的方法,求恰好抽到一男一女学生的概率?
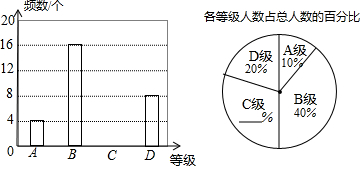
分析 (1)首先用A等级的学生人数除以A等级的人数所占的百分比,求出总人数;然后用总人数减去A、B、D三个等级的人数,求出C等级的人数,补全条形图;用C等级的人数除以总人数,得出C等级的人数所占的百分比,补全扇形图;
(2)用加权平均数的计算公式求解即可;
(3)若A等级的4名学生中有2名男生2名女生,现从中任意选取2名参加学校培训班,应用列表法的方法,求出恰好选到1名男生和1名女生的概率是多少即可.
解答 解:(1)4÷10%=40(人),
C等级的人数40-4-16-8=12(人),
C等级的人数所占的百分比12÷40=30%.
两个统计图补充如下:
(2)9×10%+8×40%+7×30%+6×20%=7.4(分);
(3)列表为:
| 男1 | 男2 | 女1 | 女2 | |
| 男1 | -- | 男2男1 | 女1男1 | 女2男1 |
| 男2 | 男1男2 | -- | 女1男2 | 女2男2 |
| 女1 | 男1女1 | 男2女1 | -- | 女2女1 |
| 女2 | 男1女2 | 男2女2 | 女1女2 | -- |
所以恰好选到1名男生和1名女生的概率P=$\frac{8}{12}$=$\frac{2}{3}$.
点评 此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.也考查了扇形统计图、条形统计图的应用以及加权平均数.

练习册系列答案
相关题目
 如图,P为矩形ABCD内一点,求证:S△PBC=S△PAC+S△PCD.
如图,P为矩形ABCD内一点,求证:S△PBC=S△PAC+S△PCD.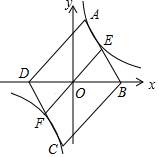 如图,点B,D分别在x轴的正、负半轴上,OB=OD,以BD为对角线作?ABCD,使点A、C分别落在反比例函数y=$\frac{k}{x}$的第一、三象限的图象上,且S?ABCD=28.AB、CD分别交反比例图象于点E、F,连结EF.当四边形BEFC是平行四边形时,k的值是$\frac{14}{3}$.
如图,点B,D分别在x轴的正、负半轴上,OB=OD,以BD为对角线作?ABCD,使点A、C分别落在反比例函数y=$\frac{k}{x}$的第一、三象限的图象上,且S?ABCD=28.AB、CD分别交反比例图象于点E、F,连结EF.当四边形BEFC是平行四边形时,k的值是$\frac{14}{3}$.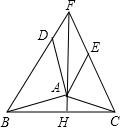 如图,△ABC中,分别以AB、AC为边向三角形外作△ABD和△ACE,使AD=AB,AE=AC,∠BAD=∠CAE=90°,AH⊥BC,H为垂足,点F在HA的延长线上,且AF=BC,求证:四边形AEFD是平行四边形.
如图,△ABC中,分别以AB、AC为边向三角形外作△ABD和△ACE,使AD=AB,AE=AC,∠BAD=∠CAE=90°,AH⊥BC,H为垂足,点F在HA的延长线上,且AF=BC,求证:四边形AEFD是平行四边形.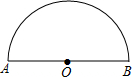 如图,AB是半圆O的直径,且AB=4cm,动点P从点O出发,沿OA→$\widehat{AB}$→BO的路径以每秒1cm的速度运动一周.设运动时间为t,s=OP2,则下列图象能大致刻画s与t的关系的是( )
如图,AB是半圆O的直径,且AB=4cm,动点P从点O出发,沿OA→$\widehat{AB}$→BO的路径以每秒1cm的速度运动一周.设运动时间为t,s=OP2,则下列图象能大致刻画s与t的关系的是( )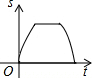



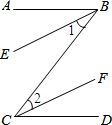 (1)完成下面的推理说明:
(1)完成下面的推理说明: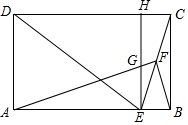 如图,在矩形ABCD中,E为AB边上一点,EC平分∠DEB,F为CE的中点,连接AF,BF,过点E作EH∥BC分别交AF,CD于G,H两点.
如图,在矩形ABCD中,E为AB边上一点,EC平分∠DEB,F为CE的中点,连接AF,BF,过点E作EH∥BC分别交AF,CD于G,H两点. 如图,正方形ABCD中内接正三角形AEF.求证:S△EFC=S△ABE+S△ADF.
如图,正方形ABCD中内接正三角形AEF.求证:S△EFC=S△ABE+S△ADF.