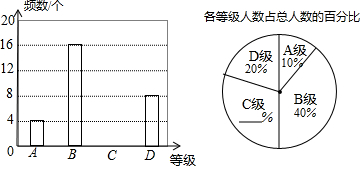
题目内容
1.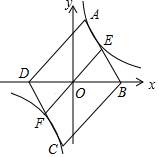 如图,点B,D分别在x轴的正、负半轴上,OB=OD,以BD为对角线作?ABCD,使点A、C分别落在反比例函数y=$\frac{k}{x}$的第一、三象限的图象上,且S?ABCD=28.AB、CD分别交反比例图象于点E、F,连结EF.当四边形BEFC是平行四边形时,k的值是$\frac{14}{3}$.
如图,点B,D分别在x轴的正、负半轴上,OB=OD,以BD为对角线作?ABCD,使点A、C分别落在反比例函数y=$\frac{k}{x}$的第一、三象限的图象上,且S?ABCD=28.AB、CD分别交反比例图象于点E、F,连结EF.当四边形BEFC是平行四边形时,k的值是$\frac{14}{3}$.
分析 连接OA,如图,利用平行四边形的性质得AB=CD,AB∥CD,则∠ABD=∠CDB,再证明△OBE≌△ODF得到BE=DF,接着利用四边形BEFC为平行四边形得到BE=CF,所以AE=BE,设A(t,$\frac{k}{t}$),E点的纵坐标为$\frac{k}{2t}$,则E(2t,$\frac{k}{2t}$),所以B(3t,0),然后利用△OAB的面积为7得到$\frac{1}{2}$•3t•$\frac{k}{t}$=7,从而可得到k的值.
解答 解:连接OA,如图,
∵四边形ABCD为平行四边形,
∴AB=CD,AB∥CD,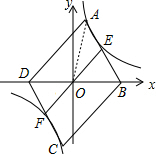
∴∠ABD=∠CDB,
在△OBE和△ODF中
$\left\{\begin{array}{l}{∠OBE=∠ODF}\\{OB=OD}\\{∠BOE=∠DOF}\end{array}\right.$,
∴△OBE≌△ODF,
∴BE=DF,
∵四边形BEFC为平行四边形,
∴BE=CF,
∴AE=BE,
即点E为AB的中点,
设A(t,$\frac{k}{t}$),则E(2t,$\frac{k}{2t}$),
∴B(3t,0),
∵S?ABCD=28.
∴△OAB的面积为7,
∴$\frac{1}{2}$•3t•$\frac{k}{t}$=7,
∴k=$\frac{14}{3}$.
故答案为$\frac{14}{3}$.
点评 本题考查了反比例函数比例系数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|k|,且保持不变.也考查了平行四边形的性质.

①四边相等的四边形一定是菱形
②顺次连接矩形各边中点形成的四边形一定是正方形
③对角线相等的四边形一定是矩形
④经过平行四边形对角线交点的直线,一定能把平行四边形分成面积相等的两部分
其中正确的有( )个.
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
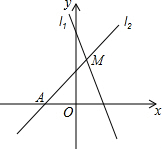 如图,已知直线l1:y=-2x+4与直线l2:y=kx+b(k≠0)在第一象限交于点M.若直线l2与x轴的交点为A(-2,0),则k的取值范围是( )
如图,已知直线l1:y=-2x+4与直线l2:y=kx+b(k≠0)在第一象限交于点M.若直线l2与x轴的交点为A(-2,0),则k的取值范围是( )| A. | -2<k<2 | B. | -2<k<0 | C. | 0<k<4 | D. | 0<k<2 |
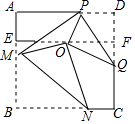 如图,正方形纸片ABCD的边长为6,E为AB的三等分点,F为DC的三等分点,O为EF中点,将正方形纸片折叠使R与O重合,折痕为MN,使D与O重合,折痕为PQ,连接PM,则PM=$\frac{115}{24}$.
如图,正方形纸片ABCD的边长为6,E为AB的三等分点,F为DC的三等分点,O为EF中点,将正方形纸片折叠使R与O重合,折痕为MN,使D与O重合,折痕为PQ,连接PM,则PM=$\frac{115}{24}$. 如图,在菱形ABCD中,AB=6cm,∠A=60°,点E以1cm/s的速度沿AB边由A向B匀速运动,同时点F以2cm/s的速度沿CB边由C向B运动,F到达点B时两点同时停止运动.设运动时间为t秒,当△DEF为等边三角形时,t的值为( )
如图,在菱形ABCD中,AB=6cm,∠A=60°,点E以1cm/s的速度沿AB边由A向B匀速运动,同时点F以2cm/s的速度沿CB边由C向B运动,F到达点B时两点同时停止运动.设运动时间为t秒,当△DEF为等边三角形时,t的值为( )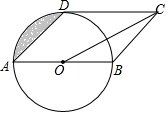 如图,四边形ABCD是平行四边形,以AB为直径的⊙O与CD相切于点D,若OC=2$\sqrt{5}$,则图中阴影部分的面积为π-2.
如图,四边形ABCD是平行四边形,以AB为直径的⊙O与CD相切于点D,若OC=2$\sqrt{5}$,则图中阴影部分的面积为π-2.