题目内容
20．
如图，P为矩形ABCD内一点，求证：S△PBC=S△PAC+S△PCD．
分析 由矩形的性质得出S△APD+S△BPC=S△ABP+S△CPD=$\frac{1}{2}$S矩形ABCD，S△ADC=S△ABC=$\frac{1}{2}$S矩形ABCD，得出S△PBC=$\frac{1}{2}$S矩形ABCD-S△APD，S△PAC+S△PCD=S△ADC-S△APD=$\frac{1}{2}$S矩形ABCD-S△APD，即可得出结论．
解答 证明：∵四边形ABCD是矩形，
∴S△APD+S△BPC=$\frac{1}{2}$S矩形ABCD，S△ABP+S△CPD=$\frac{1}{2}$S矩形ABCD，S△ADC=S△ABC=$\frac{1}{2}$S矩形ABCD，
∴S△PBC=$\frac{1}{2}$S矩形ABCD-S△APD，S△PAC+S△PCD=S△ADC-S△APD=$\frac{1}{2}$S矩形ABCD-S△APD，
∴S△PBC=S△PAC+S△PCD．
点评 本题主要考查矩形的性质、三角形的面积关系，熟练掌握矩形的性质是解决问题的关键．
练习册系列答案
相关题目
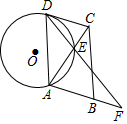已知，如图，四边形ABCD是平行四边形，⊙O与边DC相切于点D，交对角线AC于点E，连接DE并延长交AB的延长线于点F，且AE=DE．
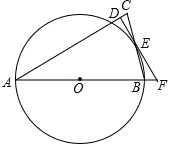如图1，以△ABC的边AB为直径的⊙O交边BC于点E，过点E作O的切线交AC于点D，且ED⊥AC．
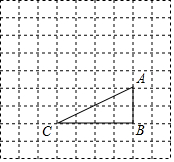如图，在边长为1的正方形网格中，△ABC的顶点均在格点上，点A、B的坐标分别是A（5，3）、B（5，1）．
如图，正方形纸片ABCD的边长为6，E为AB的三等分点，F为DC的三等分点，O为EF中点，将正方形纸片折叠使R与O重合，折痕为MN，使D与O重合，折痕为PQ，连接PM，则PM=$\frac{115}{24}$．