题目内容
17.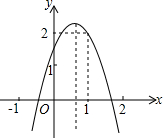 如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1,x2,其中-1<x1<0,1<x2<2.下列结论:①4a+2b+c<0;②a<-1;③b2+8a>4ac;④2a-b<0.其中结论正确的有①②③④.(把所有正确答案的序号都填写在横线上)
如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1,x2,其中-1<x1<0,1<x2<2.下列结论:①4a+2b+c<0;②a<-1;③b2+8a>4ac;④2a-b<0.其中结论正确的有①②③④.(把所有正确答案的序号都填写在横线上)
分析 由抛物线可知当x=2时y<0,x=-1时y<0,则有4a+2b+c<0,a-b+c<0;由抛物线过(1,2)可得a+b+c=2;由抛物线的开口方向可得a<0;由抛物线的顶点位置和对称轴位置可得$\frac{4ac-{b}^{2}}{4a}$,$-\frac{b}{2a}$>0;然后进行推理,即可对各个结论作出判断.
解答 解:由二次函数的图象可得:当x=2时y<0,则有4a+2b+c<0(1),故①正确;
∵二次函数的图象经过点(1,2),
∴a+b+c=2(2),
由二次函数的图象可得:当x=-1时,y<0,则有a-b+c<0(3),
把(2)代入(1)得到2+3a+b<0,则有a<$\frac{-b-2}{3}$,
把(2)代入(3)得到2-2b<0,则有b>1,
则a<-1,故②正确;
由二次函数的图象中顶点的位置,可得:$\frac{4ac-{b}^{2}}{4a}$>2(4),
由抛物线开口向下,可得:a<0,
则由(4)可得4ac-b2<8a,即b2+8a>4ac,故③正确;
由抛物线的对称轴的位置,可得$-\frac{b}{2a}$>0,则b>0,
又由a<0,则有2a-b<0,故④正确;
故答案为:①②③④.
点评 本题考查了二次函数图象与系数的关系.解答此类问题的关键是根据图象得出开口方向、对称轴、与坐标轴的交点与系数个关系,自变量取±1,±2时的函数值的符号,利用所得的等式或不等式变形.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
7.具备下列条件的△ABC中,不是直角三角形的是( )
| A. | ∠A+∠B=∠C | B. | ∠A=$\frac{1}{2}$∠B=$\frac{1}{3}$∠C | C. | ∠A:∠B:∠C=1:2:3 | D. | ∠A=2∠B=3∠C |
 如图,已知等腰△ABC,AB=AC,设AB=x,BC=y,回答下列问题:
如图,已知等腰△ABC,AB=AC,设AB=x,BC=y,回答下列问题: