题目内容
7.计算:(1)$\frac{m-p}{m-n}+\frac{n-p}{n-m}$
(2)$-\frac{m^2}{n}÷\frac{n^2}{m^3}•\frac{m}{n^2}$
(3)$(1+\frac{1}{x-1})÷\frac{x}{{{x^2}-1}}$
(4)$\frac{1}{2m}-\frac{1}{m+n}•(\frac{m+n}{2m}-m-n)$.
分析 (1)原式变形后,利用同分母分式的减法法则计算即可得到结果;
(2)原式利用除法法则变形,约分即可得到结果;
(3)原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分即可得到结果;
(4)原式括号中两项通分并利用同分母分式的减法法则计算,约分后利用同分母分式的减法法则计算即可得到结果.
解答 解:(1)原式=$\frac{m-p-n+p}{m-n}$=$\frac{m-n}{m-n}$=1;
(2)原式=-$\frac{{m}^{2}}{n}$•$\frac{{m}^{3}}{{n}^{2}}$•$\frac{m}{{n}^{2}}$=-$\frac{{m}^{6}}{{n}^{5}}$;
(3)原式=$\frac{x-1+1}{x-1}$•$\frac{(x+1)(x-1)}{x}$=$\frac{x}{x-1}$•$\frac{(x+1)(x-1)}{x}$=x+1;
(4)原式=$\frac{1}{2m}$-$\frac{1}{m+n}$•$\frac{m+n-2m(m+n)}{2m}$=$\frac{1}{2m}$-$\frac{1}{m+n}$•$\frac{(m+n)(1-2m)}{2m}$=$\frac{1-1+2m}{2m}$=1.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
16.若x+y=7,xy=-8,下列各式计算结果不正确的是( )
| A. | (x+y)2=49 | B. | x2+y2=65 | C. | (x-y)2=81 | D. | (xy)2=-64 |
17.|$\sqrt{2}$-$\sqrt{3}$|=( )
| A. | $\sqrt{2}$+$\sqrt{3}$ | B. | $\sqrt{2}$-$\sqrt{3}$ | C. | -$\sqrt{2}$-$\sqrt{3}$ | D. | $\sqrt{3}$-$\sqrt{2}$ |
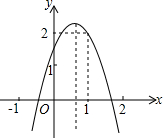 如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1,x2,其中-1<x1<0,1<x2<2.下列结论:①4a+2b+c<0;②a<-1;③b2+8a>4ac;④2a-b<0.其中结论正确的有①②③④.(把所有正确答案的序号都填写在横线上)
如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1,x2,其中-1<x1<0,1<x2<2.下列结论:①4a+2b+c<0;②a<-1;③b2+8a>4ac;④2a-b<0.其中结论正确的有①②③④.(把所有正确答案的序号都填写在横线上) 如图,将三角尺直角顶点放在直尺一边上,∠1=30°,∠2=55°,则∠3度数=25°.
如图,将三角尺直角顶点放在直尺一边上,∠1=30°,∠2=55°,则∠3度数=25°. 如图,已知AC平分∠DAB,∠1=∠2.∠B=60°,求∠BCD的度数?
如图,已知AC平分∠DAB,∠1=∠2.∠B=60°,求∠BCD的度数?