题目内容
8.若$\frac{a}{5}=\frac{b}{3}=\frac{c}{4}≠0$,则$\frac{a+b+c}{b}$=4.分析 先设$\frac{a}{5}=\frac{b}{3}=\frac{c}{4}=k$,可得a=5k,b=3k,c=4k,再代入解答即可.
解答 解:设$\frac{a}{5}=\frac{b}{3}=\frac{c}{4}=k$,
可得a=5k,b=3k,c=4k,
把=5k,b=3k,c=4k代入$\frac{a+b+c}{b}$=$\frac{5k+3k+4k}{3k}$=4,
故答案为:4.
点评 本题考查了比例的性质.已知几个量的比值时,常用的解法是:设一个未知数,把题目中的几个量用所设的未知数表示出来,实现消元.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.下列运算正确的是( )
| A. | $\sqrt{18}÷\sqrt{2}=9$ | B. | ${(\frac{1}{3})}^{-2}=\frac{1}{9}$ | C. | (-a2)3=a6 | D. | a6÷($\frac{1}{2}$a2)=2a4 |
13.下列各式中,正确的是( )
| A. | $\sqrt{(-2)^{2}}$=2 | B. | -$\sqrt{3.6}$=-0.6 | C. | $\sqrt{(-13)^{2}}$=-13 | D. | $\sqrt{36}$=±6 |
20.在平面直角坐标系中,一次函数y=-3x+1的图象所经过的象限是( )
| A. | 二、三、四 | B. | 一、三、四 | C. | 一、二、四 | D. | 一、二、三 |
 如图是一个长方形纸条折成的图形,已知图中∠2=122°,则∠1=116°.
如图是一个长方形纸条折成的图形,已知图中∠2=122°,则∠1=116°.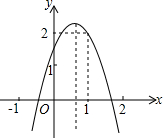 如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1,x2,其中-1<x1<0,1<x2<2.下列结论:①4a+2b+c<0;②a<-1;③b2+8a>4ac;④2a-b<0.其中结论正确的有①②③④.(把所有正确答案的序号都填写在横线上)
如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1,x2,其中-1<x1<0,1<x2<2.下列结论:①4a+2b+c<0;②a<-1;③b2+8a>4ac;④2a-b<0.其中结论正确的有①②③④.(把所有正确答案的序号都填写在横线上) 如图,将三角尺直角顶点放在直尺一边上,∠1=30°,∠2=55°,则∠3度数=25°.
如图,将三角尺直角顶点放在直尺一边上,∠1=30°,∠2=55°,则∠3度数=25°.