题目内容
6. 如图,已知等腰△ABC,AB=AC,设AB=x,BC=y,回答下列问题:
如图,已知等腰△ABC,AB=AC,设AB=x,BC=y,回答下列问题:(1)若x、y满足x2+y2-6x-4y+13=0,请求出△ABC的周长.
(2)若△ABC的周长是12
(Ⅰ)列出关于x、y的二元一次方程;
(Ⅱ)求出该方程所有符合要求的正整数解.
分析 (1)直接利用完全平方方公式进而求出x,y的值进而求出即可;
(2)(I)利用三角形周长公式求出即可;
(II)直接利用二元一次方程的整数解求法得出即可.
解答 解:(1)x2+y2-6x-4y+13=0,
(x-3)2+(y-2)2=0,
则x=3,y=2,
故△ABC的周长为:3+3+2=8;
(2)(I)∵AB=x,BC=y,
∴2x+y=12;
(II)当x=4时,y=4,当x=5时,y=2,
即方程组的正整数解为:$\left\{\begin{array}{l}{x=4}\\{y=4}\end{array}\right.$,$\left\{\begin{array}{l}{x=5}\\{y=2}\end{array}\right.$.
点评 此题主要考查了二元一次方程的应用以及等腰三角形的性质,正确应用等腰三角形的性质是解题关键.

练习册系列答案
相关题目
11.已知两条线段长分别为3、4,那么能与它们组成直角三角形的第三条线段长是( )
| A. | 5 | B. | $\sqrt{7}$ | C. | 5或$\sqrt{7}$ | D. | 不能确定 |
16.若x+y=7,xy=-8,下列各式计算结果不正确的是( )
| A. | (x+y)2=49 | B. | x2+y2=65 | C. | (x-y)2=81 | D. | (xy)2=-64 |
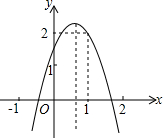 如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1,x2,其中-1<x1<0,1<x2<2.下列结论:①4a+2b+c<0;②a<-1;③b2+8a>4ac;④2a-b<0.其中结论正确的有①②③④.(把所有正确答案的序号都填写在横线上)
如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1,x2,其中-1<x1<0,1<x2<2.下列结论:①4a+2b+c<0;②a<-1;③b2+8a>4ac;④2a-b<0.其中结论正确的有①②③④.(把所有正确答案的序号都填写在横线上) 如图,将三角尺直角顶点放在直尺一边上,∠1=30°,∠2=55°,则∠3度数=25°.
如图,将三角尺直角顶点放在直尺一边上,∠1=30°,∠2=55°,则∠3度数=25°.