题目内容
如图①,直线y=2x-4分别交坐标轴于B,A两点,交双曲线y=
(x>0)于C点,S△AOC=8.
(1)求双曲线的解析式;
(2)直线y=mx-4(m>0)交x轴于D点.若直线AC平分△AOD的周长,求m的值;
(3)如图②,M是射线BA上的一点,将线段BM绕B点逆时针旋转135°,点M落到双曲线上的点N,求线段BN的长度.
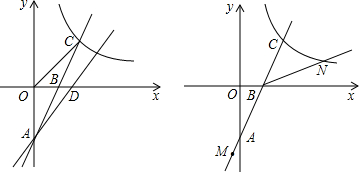
| k |
| x |
(1)求双曲线的解析式;
(2)直线y=mx-4(m>0)交x轴于D点.若直线AC平分△AOD的周长,求m的值;
(3)如图②,M是射线BA上的一点,将线段BM绕B点逆时针旋转135°,点M落到双曲线上的点N,求线段BN的长度.
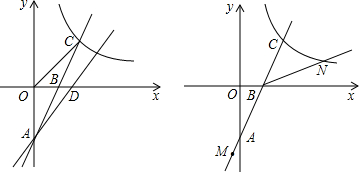
考点:反比例函数综合题
专题:
分析:(1)求出点A、B的坐标,设点C的坐标为(a,2a-4),然后根据S△AOC=8,求出m的值,求出点C的坐标,继而可求得反比例函数的解析式;
(2)设点D的坐标为(
,0),求出点B的坐标,然后根据题意可得AO+BO=BD+AD,代入求出m的值;
(3)作BD⊥OC于D,NE⊥x轴于E,根据(1)可得∠BOC=45°,设BE=t,则OE=t+2,表示出N点坐标,在Rt△OBD中求出OD、BD、CD的值,利用三角形的相似代入数值求出t的值,最后利用勾股定理求得BN的长度.
(2)设点D的坐标为(
| 4 |
| m |
(3)作BD⊥OC于D,NE⊥x轴于E,根据(1)可得∠BOC=45°,设BE=t,则OE=t+2,表示出N点坐标,在Rt△OBD中求出OD、BD、CD的值,利用三角形的相似代入数值求出t的值,最后利用勾股定理求得BN的长度.
解答:
解:(1)把x=0代入y=2x-4得y=4,
则A点坐标为(0,-4),
把y=0代入y=2x-4得2x-4=0,解得x=2,
则B点坐标为(2,0),
设C点坐标为(a,2a-4),
∵S△AOC=8,
∴
×4×a=8,
解得a=4,
∴C点坐标为(4,4),
∴k=4×4=16,即反比例函数解析式为y=
;
(2)由(1)得,直线AC的解析式为:y=2x-4,
则点B的坐标为(2,0),
设点D的坐标为(
,0),
则BO=2,BD=
-2,AD=
=4
,
∵AO+BO=BD+AD,
∴6=
-2+4
,
解得:m=
;
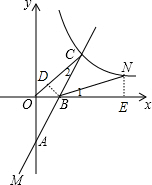
(3)作BD⊥OC于D,NE⊥x轴于E,如图,
由(1)得,∠BOC=45°,OC=4
,
设BE=t,则OE=t+2,
则N点坐标表示为(t+2,
),即NE=
,
在Rt△OBD中,
∵OB=2,∠BOD=45°,
∴OD=BD=
OB=
,
∴CD=OC-OD=3
,
∵线段BM绕B点逆时针旋转135°,M落在双曲线上的点N处,
∴∠MBN=135°,BN=BM,
∴∠CBN=45°,
∵∠CBN+∠1=∠BOC+∠2,
∴∠1=∠2,
∴Rt△BEN∽Rt△CDB,
∴
=
,即
=
,
整理得t2+2t-48=0,
解得t1=-8(舍去),t2=6,
∴BE=6,NE=
=2,
在Rt△BEN中,
BN=
=2
.
则A点坐标为(0,-4),
把y=0代入y=2x-4得2x-4=0,解得x=2,
则B点坐标为(2,0),
设C点坐标为(a,2a-4),
∵S△AOC=8,
∴
| 1 |
| 2 |
解得a=4,
∴C点坐标为(4,4),
∴k=4×4=16,即反比例函数解析式为y=
| 16 |
| x |
(2)由(1)得,直线AC的解析式为:y=2x-4,
则点B的坐标为(2,0),
设点D的坐标为(
| 4 |
| m |
则BO=2,BD=
| 4 |
| m |
16+
|
1+
|

∵AO+BO=BD+AD,
∴6=
| 4 |
| m |
1+
|
解得:m=
| 4 |
| 3 |
(3)作BD⊥OC于D,NE⊥x轴于E,如图,
由(1)得,∠BOC=45°,OC=4
| 2 |
设BE=t,则OE=t+2,
则N点坐标表示为(t+2,
| 16 |
| t+2 |
| 16 |
| t+2 |
在Rt△OBD中,
∵OB=2,∠BOD=45°,
∴OD=BD=
| ||
| 2 |
| 2 |
∴CD=OC-OD=3
| 2 |
∵线段BM绕B点逆时针旋转135°,M落在双曲线上的点N处,
∴∠MBN=135°,BN=BM,
∴∠CBN=45°,
∵∠CBN+∠1=∠BOC+∠2,
∴∠1=∠2,
∴Rt△BEN∽Rt△CDB,
∴
| NE |
| BD |
| BE |
| CD |
| ||
|
| t | ||
3
|
整理得t2+2t-48=0,
解得t1=-8(舍去),t2=6,
∴BE=6,NE=
| 16 |
| 2+6 |
在Rt△BEN中,
BN=
| BE2+NE2 |
| 10 |
点评:本题考查了反比例函数的综合应用,涉及了反比例函数与一次函数的交点问题、旋转的性质、等腰直角三角形的性质以及相似三角形的判定与性质,知识点较多,难度比较大.

练习册系列答案
相关题目
一元二次方程2x2+5x+3=0的实数根的情况是( )
| A、有两个不相等的实数根 |
| B、有两个相等的实数根 |
| C、有一个实数根 |
| D、没有实数根 |
 如图,已知B(0,1),C(-2,0),过点B作AB⊥BC,使得AB=BC,AB交x轴于点F.
如图,已知B(0,1),C(-2,0),过点B作AB⊥BC,使得AB=BC,AB交x轴于点F.
 如图,直线AC与x轴、y轴分别交于点C(-2,0)、A(0,4),B点坐标为(4,0),过点B作BD⊥AC于D,BD交OA于点H.
如图,直线AC与x轴、y轴分别交于点C(-2,0)、A(0,4),B点坐标为(4,0),过点B作BD⊥AC于D,BD交OA于点H.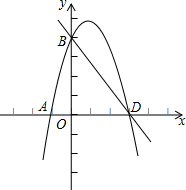 如图,在平面直角坐标系中,己知二次函数y=ax2+
如图,在平面直角坐标系中,己知二次函数y=ax2+