题目内容
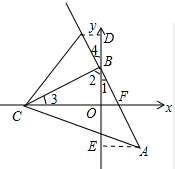
 如图,已知B(0,1),C(-2,0),过点B作AB⊥BC,使得AB=BC,AB交x轴于点F.
如图,已知B(0,1),C(-2,0),过点B作AB⊥BC,使得AB=BC,AB交x轴于点F.(1)求点A到y轴的距离;
(2)点P从A出发,以1个单位/秒的速度沿射线AB运动,运动时间为t秒,请用含有t的式子表示△ACP的面积S;
(3)在(2)的条件下,当BC平分∠PCF时,求此时P点坐标.
考点:全等三角形的判定与性质,坐标与图形性质
专题:
分析:(1)过A点作AE⊥y轴垂足为点E,根据全等三角形的判定证出△BOC≌△EA,再根据全等三角形的性质得出BE=OC,AE=OB,解答即可;
(2)先根据勾股定理求出BC,即可求出△ACP的面积S;
(3)作PD⊥y轴于D,先求出OF,再证明△PCB≌△FCB,得出PB=FB,然后证明△PBD≌△FBO,即可求出PD、OD,得出P坐标.
(2)先根据勾股定理求出BC,即可求出△ACP的面积S;
(3)作PD⊥y轴于D,先求出OF,再证明△PCB≌△FCB,得出PB=FB,然后证明△PBD≌△FBO,即可求出PD、OD,得出P坐标.
解答:
解:(1)过A点作AE⊥y轴,垂足为点E,如图所示:
则∠AEB=90°,
∵B(0,1),C(-2,0),
∴BO=1,CO=2,
∵AB⊥BC,
∴∠ABC=90°,
∴∠1+∠2=90°,
∵∠BOC=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
在△ABE和△BCO中,
,
∴△ABE≌△BCO(AAS),
∴AE=BO=1;
(2)根据题意得:AP=t,
由勾股定理得:BC=
=
,
∴△ACP的面积S=
AP•BC=
t•
=
t;
(3)作PD⊥y轴于D,如图所示,
 ∵∠ABC=90°,OB⊥CF,
∵∠ABC=90°,OB⊥CF,
根据射影定理得:BO2=CO•OF,
∴OF=
=
=
,
∵BC平分∠PCF,
∴∠PCB=∠FCB,
在△PCB和△FCB中,
,
∴△PCB≌△FCB(ASA),
∴PB=FB,
在△PBD和△FBO中,
,
∴△PBD≌△FBO(AAS),
∴BD=BO=1,PD=OF=
,
∴OD=2,
∴P(-
,2).
则∠AEB=90°,
∵B(0,1),C(-2,0),
∴BO=1,CO=2,
∵AB⊥BC,
∴∠ABC=90°,
∴∠1+∠2=90°,
∵∠BOC=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
在△ABE和△BCO中,
|
∴△ABE≌△BCO(AAS),
∴AE=BO=1;
(2)根据题意得:AP=t,
由勾股定理得:BC=
| 12+22 |
| 5 |
∴△ACP的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| ||
| 2 |
(3)作PD⊥y轴于D,如图所示,
 ∵∠ABC=90°,OB⊥CF,
∵∠ABC=90°,OB⊥CF,根据射影定理得:BO2=CO•OF,
∴OF=
| BO2 |
| CO |
| 12 |
| 2 |
| 1 |
| 2 |
∵BC平分∠PCF,
∴∠PCB=∠FCB,
在△PCB和△FCB中,
|
∴△PCB≌△FCB(ASA),
∴PB=FB,
在△PBD和△FBO中,
|
∴△PBD≌△FBO(AAS),
∴BD=BO=1,PD=OF=
| 1 |
| 2 |
∴OD=2,
∴P(-
| 1 |
| 2 |
点评:本题考查了全等三角形的判定与性质、勾股定理以及三角形面积的求法、坐标与图形性质;通过作辅助线构造三角形全等是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若x2+2(m-3)x+16是完全平方式,则m的值等于( )
| A、3 | B、-5 | C、7 | D、7或-1 |
不等式组
的整数解是( )
|
| A、2 | B、3 |
| C、2,3 | D、2,3,4 |
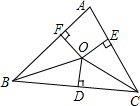 如图,O是△ABC内一点,且O到三边AB、BC、CA的距离OF=OD=OE,若∠BAC=70°,则∠BOC的度数为( )
如图,O是△ABC内一点,且O到三边AB、BC、CA的距离OF=OD=OE,若∠BAC=70°,则∠BOC的度数为( )| A、70° | B、120° |
| C、125° | D、130° |