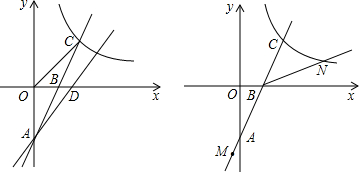题目内容
 如图,直线AC与x轴、y轴分别交于点C(-2,0)、A(0,4),B点坐标为(4,0),过点B作BD⊥AC于D,BD交OA于点H.
如图,直线AC与x轴、y轴分别交于点C(-2,0)、A(0,4),B点坐标为(4,0),过点B作BD⊥AC于D,BD交OA于点H.(1)请求点H的坐标;
(2)有两个动点P和Q分别从点C和点O同时沿x轴正方向匀速运动,速度分别为2个单位每秒和1个单位每秒,设△PQH的面积为S,点P、点Q的运动时间为t秒,请求S与t之间的函数关系式.(请直接写出相应的自变量t的取值范围);
(3)请问t为何值时,△PQH的面积是△B0H的面积的
| 1 |
| 4 |
考点:一次函数综合题
专题:
分析:(1)证明△ACO≌△BHO,求出OH=OC即可;
(2)分三种情况讨论:①当0<t<1时;②当1<t<2时;③当t>2时;以PQ为底,高为OH,分别求出S即可;
(3)先求出S△BOH,再得出S=1,代入(2)中函数关系式,即可求出t的值.
(2)分三种情况讨论:①当0<t<1时;②当1<t<2时;③当t>2时;以PQ为底,高为OH,分别求出S即可;
(3)先求出S△BOH,再得出S=1,代入(2)中函数关系式,即可求出t的值.
解答:
解:(1)∵BD⊥AC,
∴∠BDC=90°,
∵C(-2,0),A(0,4),B(4,0),
∴OA=OB=4,OC=2,
∵∠ACO+∠CAO=90°,∠ACO+∠CBD=90°,
∴∠CAO=∠CBD,
在△ACO和△BHO中,
∴△ACO≌△BHO(ASA),
∴OH=OC=2,
∴H(0,2);
(2)分三种情况讨论:
①当0<t<1时,CP=2t,OQ=t,
∴OP=2-2t,PQ=2-2t+t=2-t,
∴S=
×(2-t)×2=2-t,
∴S=2-t(0<t<1);
②当1<t<2时,CQ=2+t,CP=2t,OQ=t,
∴PQ=CQ-CP=2+t-2t=2-t,
∴S=
×(2-t)×2=2-t,
∴S=2-t(1<t<2);
③当t>2时,PQ=2t-2-t=t-2,
∴S=
×(t-2)×2=t-2,∴S=t-2(t>2);
综上所述:S=2-t(0<t<2),或S=t-2(t>2);
(3)∵S△BOH=
×2×4=4,
∴S=
S△BOH=1,
当2-t=1时,t=1;
当t-2=1时,t=3;
∴当t=1或3时,△PQH的面积是△B0H的面积的
.
∴∠BDC=90°,
∵C(-2,0),A(0,4),B(4,0),
∴OA=OB=4,OC=2,
∵∠ACO+∠CAO=90°,∠ACO+∠CBD=90°,
∴∠CAO=∠CBD,
在△ACO和△BHO中,
|
∴△ACO≌△BHO(ASA),
∴OH=OC=2,
∴H(0,2);
(2)分三种情况讨论:
①当0<t<1时,CP=2t,OQ=t,
∴OP=2-2t,PQ=2-2t+t=2-t,
∴S=
| 1 |
| 2 |
∴S=2-t(0<t<1);
②当1<t<2时,CQ=2+t,CP=2t,OQ=t,
∴PQ=CQ-CP=2+t-2t=2-t,
∴S=
| 1 |
| 2 |
∴S=2-t(1<t<2);
③当t>2时,PQ=2t-2-t=t-2,
∴S=
| 1 |
| 2 |
综上所述:S=2-t(0<t<2),或S=t-2(t>2);
(3)∵S△BOH=
| 1 |
| 2 |
∴S=
| 1 |
| 4 |
当2-t=1时,t=1;
当t-2=1时,t=3;
∴当t=1或3时,△PQH的面积是△B0H的面积的
| 1 |
| 4 |
点评:本题考查了点的坐标、函数关系式的求法、全等三角形的判定与性质以及三角形面积的计算方法;由点的坐标确定有关线段的长度和分类讨论三角形的面积是解题的关键.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
不等式组
的整数解是( )
|
| A、2 | B、3 |
| C、2,3 | D、2,3,4 |
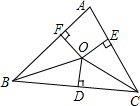 如图,O是△ABC内一点,且O到三边AB、BC、CA的距离OF=OD=OE,若∠BAC=70°,则∠BOC的度数为( )
如图,O是△ABC内一点,且O到三边AB、BC、CA的距离OF=OD=OE,若∠BAC=70°,则∠BOC的度数为( )| A、70° | B、120° |
| C、125° | D、130° |
两位数的十位数字为x,个位上的数字为y,用式子表示这个两位数是( )
| A、xy | B、x+y |
| C、10x+y | D、10y+x |