题目内容
1.从甲地到乙地有一段平路与一段上坡路,若骑自行车,平路每小时15千米,上坡每小时10千米,下坡每小时18千米,因此从甲地到乙地需29分钟,从乙地到甲地需25分钟.(1)求甲、乙两地的全程是多少千米;
(2)小明以上述速度从乙地去甲地,骑行了8分钟后接电话,需比计划提前5分钟到达甲地(接电话时间不计),求小明接电话后骑车的速度至少是每小时多少千米?
分析 (1)首先设平路所用时间为x小时,依据上坡与下坡的路程相等,列出方程,并解出方程即可得到甲地到乙地的路程;
(2)先根据(1)中的结论,求得下坡的时间,再设小明接到电话后骑车的速度至少是y千米/小时,根据比计划提前5分钟到达甲地,列出一元一次不等式,求得y的取值范围即可.
解答 解:(1)设平路所用时间为x小时,依据题意得:
10($\frac{29}{60}$-x)=18($\frac{25}{60}$-x),
解得:x=$\frac{1}{3}$,
∴甲地到乙地的路程是15×$\frac{1}{3}$+10×($\frac{29}{60}$-$\frac{1}{3}$)=6.5km;
(2)平路长15×$\frac{1}{3}$=5km,坡路长6.5-5=1.5km,
∴下坡的时间为$\frac{1.5}{18}$×60=5分钟,
设小明接到电话后骑车的速度至少是y千米/小时,依题意得:
$\frac{25-8-5}{60}$×y+15×$\frac{8-5}{60}$+1.5≥6.5,
解得y≥21.25,
∴小明接电话后骑车的速度至少是每小时21.25千米.
点评 本题主要考查了一元一次方程和一元一次不等式的应用,解决问题的关键是依据题意找出等量关系列出一元一次方程,依据不等关系列出一元一次不等式,分别求得未知数的值和取值范围.列不等式解应用题需要以“至少”、“最多”、“不超过”、“不低于”等词来体现问题中的不等关系.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 如图,△ABC中,AB=AC,PB=PC,连接AP并延长交BC于D,求证:AD垂直平分BC.
如图,△ABC中,AB=AC,PB=PC,连接AP并延长交BC于D,求证:AD垂直平分BC. (1)根据作图要求(尺规作图,保留作图痕迹,不写作法).
(1)根据作图要求(尺规作图,保留作图痕迹,不写作法).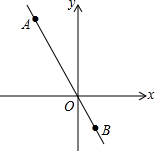 已知正比例函数y=kx(k≠0)的图象经过A(-2,4),B(1,b).求:
已知正比例函数y=kx(k≠0)的图象经过A(-2,4),B(1,b).求: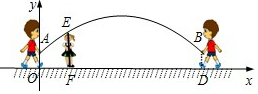 跳绳时,绳甩到最高处时的形状是抛物线.正在甩绳的甲、乙两名同学拿绳的手间距AB为6米,到地面的距离AO和BD均为0.9米,身高为1.4米的小丽站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E.以点O为原点建立如图所示的平面直角坐标系,设此抛物线的解析式为y=ax2+bx+0.9.
跳绳时,绳甩到最高处时的形状是抛物线.正在甩绳的甲、乙两名同学拿绳的手间距AB为6米,到地面的距离AO和BD均为0.9米,身高为1.4米的小丽站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E.以点O为原点建立如图所示的平面直角坐标系,设此抛物线的解析式为y=ax2+bx+0.9.