题目内容
17.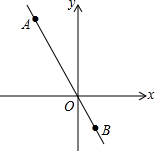 已知正比例函数y=kx(k≠0)的图象经过A(-2,4),B(1,b).求:
已知正比例函数y=kx(k≠0)的图象经过A(-2,4),B(1,b).求:(1)求k、b的值;
(2)若点C(0,2),试问在坐标轴上是否存在一点P,使PB=PC?若存在,求出P点的坐标;若不存在,请说明理由.
分析 (1)直接把A(-2,4)代入正比例函数y=kx即可得出k的值,进而可得出正比例函数的解析式,再把B(1,b)代入求出b的值即可;
(2)利用待定系数法求出直线BC的解析式,由中点坐标公式得出线段BC的中点坐标,根据PB=PC可知点P在线段BC的垂直平分线上,求出线段BC垂直平分线的解析式,进而可得出结论.
解答 解:(1)∵正比例函数y=kx(k≠0)的图象经过A(-2,4),
∴-2k=4,解得k=-2,
∴正比例函数的解析式为y=-2x.
∵B(1,b)在此函数上,
∴b=-2;
(2)∵C(0,2),B(1,-2),
∴线段BC的中点坐标为D($\frac{1}{2}$,0).
设直线BC的解析式为y=kx+d(k≠0),
∴$\left\{\begin{array}{l}{d=2}\\{k+d=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{d=2}\\{k=-4}\end{array}\right.$,
∴直线BC的解析式为:y=-4x+2.
∵PB=PC,
∴点P在线段BC的垂直平分线上,
设线段BC的垂直平分线为y=$\frac{1}{4}$x+m,
∵D($\frac{1}{2}$,0),
∴$\frac{1}{8}$+m=0,解得m=-$\frac{1}{8}$,
∴线段BC的垂直平分线为y=$\frac{1}{4}$x-$\frac{1}{8}$,
∴当x=0时,y=-$\frac{1}{8}$;
当y=0时,x=$\frac{1}{2}$,
∴P(0,-$\frac{1}{8}$)或P($\frac{1}{2}$,0).
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| a | … | 0.0001 | 0.01 | 1 | 100 | 10000 | … |
| $\sqrt{a}$ | … | 0.01 | x | 1 | y | 100 | … |
(2)从表格中探究a与数位的规律,并利用这个规律解决下面两个问题:
①已知$\sqrt{10}$≈3.16,则$\sqrt{1000}$≈31.6;
②已知$\sqrt{m}$=8.973,若$\sqrt{b}$=897.3,用含m的代数式表示b,则b=10000m;
(3)试比较$\sqrt{a}$与a的大小.
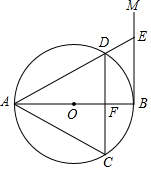 如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD∥BM,交AB于点F,且$\widehat{DA}$=$\widehat{DC}$,连接AC,AD,延长AD交BM于点E.
如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD∥BM,交AB于点F,且$\widehat{DA}$=$\widehat{DC}$,连接AC,AD,延长AD交BM于点E.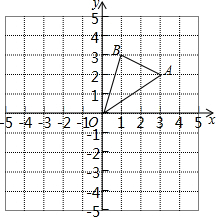 如图,△AOB的顶点均在格点上,每个小正方形的边长均为1个单位长度.
如图,△AOB的顶点均在格点上,每个小正方形的边长均为1个单位长度.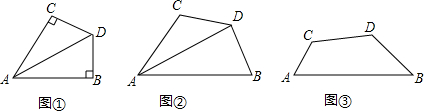
 如图,D是直径AB延长线上一点,C是圆O上一点且CO⊥AB,连接CB,DE与圆O相切于E,EF与AB相交于F.
如图,D是直径AB延长线上一点,C是圆O上一点且CO⊥AB,连接CB,DE与圆O相切于E,EF与AB相交于F. 如图所示,把△ABC绕点C顺时针旋转35°得到△A′B′C′,A′B′交AC于点D,已知∠A′DC=90°,求∠A的度数.
如图所示,把△ABC绕点C顺时针旋转35°得到△A′B′C′,A′B′交AC于点D,已知∠A′DC=90°,求∠A的度数.