题目内容
10. (1)根据作图要求(尺规作图,保留作图痕迹,不写作法).
(1)根据作图要求(尺规作图,保留作图痕迹,不写作法).①作∠BAC的平分线AD交BC于D;
②作线段AD的垂直平分线交AB于E,交AC于F,垂足为H;
③连接ED.
(2)在(1)的基础上,已知AC=16,AB=12,求△ADC的面积.
分析 (1)直接利用角平分线的作法以及线段垂直平分线的作法分别画出图形即可;
(2)结合角平分线的性质以及全等三角形的判定与性质进而结合勾股定理得出答案.
解答 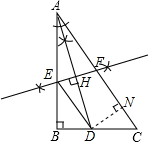 解:(1)如图所示:AD,DE,EF即为所求;
解:(1)如图所示:AD,DE,EF即为所求;
(2)过点D作DN⊥AC于点N,
∵AD是∠BAC的平分线,
∴BD=DN,
∵AC=16,AB=12,
∴BC=4$\sqrt{7}$,
在△ABD和△AND中,
$\left\{\begin{array}{l}{∠ABD=∠AND}\\{∠BAD=∠NAD}\\{AD=AD}\end{array}\right.$,
∴△ABD≌△AND(AAS),
∴AB=AN=12,
∴NC=4,
设BD=x,则DN=x,故在Rt△DNC中,
DN2+NC2=DC2,
∴x2+42=(4$\sqrt{7}$-x)2,
解得:x=$\frac{12\sqrt{7}}{7}$,
故S△ADC=$\frac{1}{2}$×$\frac{12\sqrt{7}}{7}$×16=$\frac{96\sqrt{7}}{7}$.
点评 此题主要考查了复杂作图以及平分线的性质以及全等三角形的判定与性质等知识,正确应用勾股定理是解题关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
19.数6、-1、15、-3中,最小的数是( )
| A. | 6 | B. | -1 | C. | 15 | D. | -3 |
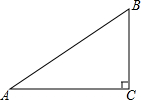 如图,在Rt△ABC中,∠C=90°,∠B=60°,AC=8,求AB的长.
如图,在Rt△ABC中,∠C=90°,∠B=60°,AC=8,求AB的长.