题目内容
2.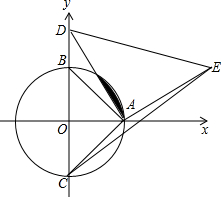 已知:如图,在平面直角坐标系xOy中,⊙O分别与坐标轴交于A、B、C三点,已知D(0,3),连接AB、AC、AD,以AD为边作△ADE(点E在第一象限),使AE=AD,∠DAE=90°.
已知:如图,在平面直角坐标系xOy中,⊙O分别与坐标轴交于A、B、C三点,已知D(0,3),连接AB、AC、AD,以AD为边作△ADE(点E在第一象限),使AE=AD,∠DAE=90°.(1)求证:△ACD≌△ABE,并说明直线BE是⊙O的切线;
(2)若∠AEB=30°,求△ADE与⊙O重叠部分的面积;
(3)连接CE,若CE=2$\sqrt{5}$,请直接写出tan∠BED的值.
分析 (1)根据SAS证明△ACD≌△ABE,得∠ACD=∠ABE,所以∠CBE=90°,即CB⊥BE,得结论;
(2)如图2,由图形可知,重叠部分面积=扇形OAF一△AOF的面积,分别求扇形的圆心角∠AOF的度数和半径OA的长,证明△OAF为等边三角形,可得结论;
(3)如图1,设BD=x,则OB=OC=3-x,根据勾股定理列方程得:BC2+BE2=CE2,即(6-x)2+(6-2x)2=(2$\sqrt{5}$)2,求出x的值可得结论.
解答  证明:(1)由题可知:AB=AC,∠BAC=90°,
证明:(1)由题可知:AB=AC,∠BAC=90°,
∵∠DAE=90°,
∴∠BAC+∠BAD=∠DAE+∠BAD.
∴∠CAD=∠BAE.
又∵AD=AE,
∴△ACD≌△ABE(SAS).
∴∠ACD=∠ABE.
∵∠ACD+∠ABC=90°,
∴∠ABE+∠ABC=90°.
∴∠CBE=90°.
∴CB⊥BE.
∴BE是⊙O的切线.
(2)如图2,由(1)△ACD≌△ABE,
∴∠ADC=∠AEB=30°,
在Rt△AOD中:∠DAO=90°-∠ADC=60°,
∵D(0,3),
∴OD=3,
tan30°=$\frac{OA}{OD}$,
∴AO=OD•tan30°=3×$\frac{\sqrt{3}}{3}$=$\sqrt{3}$,
设AD与⊙O的另一个交点为F,连结OF,
∵OA=OF,
∴△OAF为等边三角形,
∴S重叠部分=S扇形OAF-S△OAF=$\frac{60π×(\sqrt{3})^{2}}{360}$-$\frac{\sqrt{3}}{4}$×$(\sqrt{3})^{2}$=$\frac{π}{2}$-$\frac{3\sqrt{3}}{4}$;
(3)如图1,设BD=x,则OB=OC=3-x,
由(1)△ACD≌△ABE,
∴BE=CD=x+3-x+3-x=6-x,
在Rt△BCE中,由勾股定理得:BC2+BE2=CE2,
即(6-x)2+(6-2x)2=(2$\sqrt{5}$)2,
5x2-36x+52=0,
(x-2)(5x-26)=0,
x1=2,x2=$\frac{26}{5}$>3(舍去),
∴BD=2,BE=6-x=6-2=4,
在Rt△BDE中,tan∠BED=$\frac{BD}{BE}$=$\frac{2}{4}$,
∴tan∠BED=$\frac{1}{2}$.
点评 本题是圆的综合题,考查了切线的判定、三角形全等的性质和判定、扇形的面积、特殊的三角函数值、勾股定理,一元二次方程等知识,难度适中,本题要掌握两点:①阴影部分的面积可以利用和或差求解;②线段的长通常利用勾股定理列方程求解.

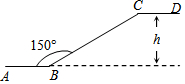 某商场一楼与二楼之间的手扶电梯如图所示.其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是( )
某商场一楼与二楼之间的手扶电梯如图所示.其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是( )| A. | 4$\sqrt{3}$m | B. | 8m | C. | $\frac{8}{3}$$\sqrt{3}$m | D. | 4m |
| A. | L=10+0.5P | B. | L=10+5P | C. | L=80+0.5P | D. | L=80+5P |
| A. | 1.13×104m | B. | 1.13×105m | C. | 11.3×104m | D. | 113×103m |
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
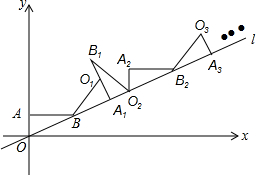 如图,直线l经过平面直角坐标系的原点O,且与x轴正方向的夹角是30°,点A的坐标是(0,1),点B在直线l上,且AB∥x轴,则点B的坐标是($\sqrt{3}$,1),现将△ABO绕点B顺时针旋转到△A1BO1的位置,使点A的对应点A1落在直线l上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线l上,顺次旋转下去…,则点A6的横坐标是$\frac{9}{2}$+$\frac{9}{2}\sqrt{3}$.
如图,直线l经过平面直角坐标系的原点O,且与x轴正方向的夹角是30°,点A的坐标是(0,1),点B在直线l上,且AB∥x轴,则点B的坐标是($\sqrt{3}$,1),现将△ABO绕点B顺时针旋转到△A1BO1的位置,使点A的对应点A1落在直线l上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线l上,顺次旋转下去…,则点A6的横坐标是$\frac{9}{2}$+$\frac{9}{2}\sqrt{3}$.
 如图,以△ABC的边BC为直径的圆O分别交AB,AC于点D,E,连接OD、OE.若
如图,以△ABC的边BC为直径的圆O分别交AB,AC于点D,E,连接OD、OE.若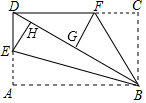 如图,将边长分别为6,2$\sqrt{3}$的矩形硬纸片ABCD折叠,使AB,CB均落在对角线BD上,点A与点H重合,点C与点G重合,折痕分别为BE,BF.下面三个结论:①∠EBF=45°;②FG是BD的垂直平分线;③DF=5.其中正确的结论是①②(只填序号)
如图,将边长分别为6,2$\sqrt{3}$的矩形硬纸片ABCD折叠,使AB,CB均落在对角线BD上,点A与点H重合,点C与点G重合,折痕分别为BE,BF.下面三个结论:①∠EBF=45°;②FG是BD的垂直平分线;③DF=5.其中正确的结论是①②(只填序号)