题目内容
13.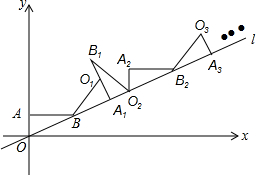 如图,直线l经过平面直角坐标系的原点O,且与x轴正方向的夹角是30°,点A的坐标是(0,1),点B在直线l上,且AB∥x轴,则点B的坐标是($\sqrt{3}$,1),现将△ABO绕点B顺时针旋转到△A1BO1的位置,使点A的对应点A1落在直线l上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线l上,顺次旋转下去…,则点A6的横坐标是$\frac{9}{2}$+$\frac{9}{2}\sqrt{3}$.
如图,直线l经过平面直角坐标系的原点O,且与x轴正方向的夹角是30°,点A的坐标是(0,1),点B在直线l上,且AB∥x轴,则点B的坐标是($\sqrt{3}$,1),现将△ABO绕点B顺时针旋转到△A1BO1的位置,使点A的对应点A1落在直线l上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线l上,顺次旋转下去…,则点A6的横坐标是$\frac{9}{2}$+$\frac{9}{2}\sqrt{3}$.
分析 先根据点A的坐标是(0,1),∠ABO=30°,AB∥x轴,即可得到AB=$\sqrt{3}$,AO=1,进而得出点B的坐标;根据△ABO旋转后与直线l重合的边的长度,依次求出点A1,A2,A3,A4,A5,A6的横坐标,即可解决问题.
解答  解:∵点A的坐标是(0,1),∠ABO=30°,AB∥x轴,
解:∵点A的坐标是(0,1),∠ABO=30°,AB∥x轴,
∴AB=$\sqrt{3}$,AO=1,
∴点B的坐标为($\sqrt{3}$,1),
由题可得,A1的横坐标为$\frac{3}{2}$+$\sqrt{3}$,
A2的横坐标为$\frac{3}{2}$+$\frac{3}{2}\sqrt{3}$,
A3的横坐标为3+$\frac{5}{2}\sqrt{3}$,
A4的横坐标为3+3$\sqrt{3}$,
A5的横坐标为$\frac{9}{2}$+4$\sqrt{3}$,
A6的横坐标为$\frac{9}{2}$+$\frac{9}{2}\sqrt{3}$,
故答案为:($\sqrt{3}$,1),$\frac{9}{2}$+$\frac{9}{2}\sqrt{3}$.
点评 本题考查坐标与图形的变换-旋转,一次函数图形与几何变换等知识的运用,解题的关键是学会从特殊到一般,探究规律,由规律解决问题.

练习册系列答案
相关题目
16.不等式-2x>$\frac{1}{2}$的解集是( )
| A. | x<-$\frac{1}{4}$ | B. | x<-1 | C. | x>-$\frac{1}{4}$ | D. | x>-1 |
5.sin60°的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
3. 如图,函数y=2x和y=ax+4的图象相交于点A(m,2),则不等式2x<ax+4的解集为( )
如图,函数y=2x和y=ax+4的图象相交于点A(m,2),则不等式2x<ax+4的解集为( )
 如图,函数y=2x和y=ax+4的图象相交于点A(m,2),则不等式2x<ax+4的解集为( )
如图,函数y=2x和y=ax+4的图象相交于点A(m,2),则不等式2x<ax+4的解集为( )| A. | x>3 | B. | x<1 | C. | x>1 | D. | x<3 |
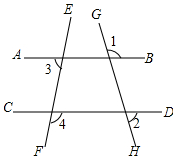 如图,已知直线AB、CD与直线EF、GH相交,且∠1+∠2=180°,∠3=70°,求∠4的度数.
如图,已知直线AB、CD与直线EF、GH相交,且∠1+∠2=180°,∠3=70°,求∠4的度数.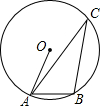 如图,A,B,C是⊙O上的三点,若∠BAO=65°,则∠ACB的度数是25°.
如图,A,B,C是⊙O上的三点,若∠BAO=65°,则∠ACB的度数是25°.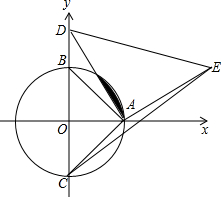 已知:如图,在平面直角坐标系xOy中,⊙O分别与坐标轴交于A、B、C三点,已知D(0,3),连接AB、AC、AD,以AD为边作△ADE(点E在第一象限),使AE=AD,∠DAE=90°.
已知:如图,在平面直角坐标系xOy中,⊙O分别与坐标轴交于A、B、C三点,已知D(0,3),连接AB、AC、AD,以AD为边作△ADE(点E在第一象限),使AE=AD,∠DAE=90°.