题目内容
20.已知抛物线y=-(x+2)2,当x>-2时,y随x的增大而增大,当x<-2时.y随x的增大而减小,当x=-2时,y取得最大值为0.分析 由抛物线解析式可得出其对称轴、开口方向及顶点坐标,根据增减性可求得答案.
解答 解:
∵y=-(x+2)2,
∴抛物线开口向下,对称轴为x=-2,
∴当x<-2时,y随x的增大而增大,当x>-2时,y随x的增大而减小,
∴当x=-2时,y取得最大值0,
故答案为:x<-2;x>-2;-2;0.
点评 本题主要考查二次函数的性质,掌握抛物线的顶点式是解题的关键,即在y=a(x-h)2+k中,对称轴为x=h,顶点坐标为(h,k).

练习册系列答案
相关题目
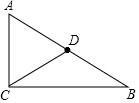 如图,在Rt△ABC中,∠C=90°,AC=9cm,BC=12cm,点D是AB的中点,现在以C点为圆心画圆,使A,B,D三点满足一点在⊙C外,一点在⊙C上,一点在⊙C内,求⊙C的半径.
如图,在Rt△ABC中,∠C=90°,AC=9cm,BC=12cm,点D是AB的中点,现在以C点为圆心画圆,使A,B,D三点满足一点在⊙C外,一点在⊙C上,一点在⊙C内,求⊙C的半径.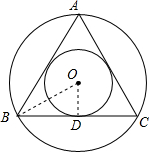 已知,正三角形ABC的边长为1,正三角形ABC的外接圆和它的内切圆是同心圆,求这两个圆所形成的圆环的面积.
已知,正三角形ABC的边长为1,正三角形ABC的外接圆和它的内切圆是同心圆,求这两个圆所形成的圆环的面积.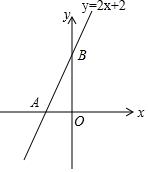 如图所示,直线y=2x+2与x轴交于点A,与y轴交于点B.
如图所示,直线y=2x+2与x轴交于点A,与y轴交于点B.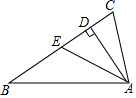 如图,在△ABC中,∠CAB=90°,AD⊥BC,AE是BC边上的中线,4DE=BC,求∠C的度数.
如图,在△ABC中,∠CAB=90°,AD⊥BC,AE是BC边上的中线,4DE=BC,求∠C的度数. 如图,已知OA=OC,OB=OD,∠AOC=∠BOD,求证:∠A=∠C.
如图,已知OA=OC,OB=OD,∠AOC=∠BOD,求证:∠A=∠C.