题目内容
18. 如图,已知四边形PQRS是菱形,PE=7,EF=6,PF=5,则ER=$\frac{7}{2}$.
如图,已知四边形PQRS是菱形,PE=7,EF=6,PF=5,则ER=$\frac{7}{2}$.
分析 根据四边形PQRS是菱形,得到QR=PQ,QR∥PF,推出△ERQ∽△EFP,于是得到$\frac{QR}{PF}=\frac{EQ}{EP}=\frac{ER}{EF}$,设QR=PQ=x,EQ=y,ER=z,得到$\frac{x}{5}=\frac{y}{7}=\frac{z}{6}=k$,求得x=5k,y=7k,z=6k,由于EQ+PQ=x+y=5k+7k=12k=7=PE,得到k=$\frac{7}{12}$,即可得到结果.
解答 解:∵ 四边形PQRS是菱形,
四边形PQRS是菱形,
∴QR=PQ,QR∥PF,
∴$\frac{QR}{PF}=\frac{EQ}{EP}=\frac{ER}{EF}$,
∵PE=7,EF=6,PF=5,
设QR=PQ=x,EQ=y,ER=z,
∴$\frac{x}{5}=\frac{y}{7}=\frac{z}{6}=k$,
∴x=5k,y=7k,z=6k,
∵EQ+PQ=x+y=5k+7k=12k=7=PE,
∴k=$\frac{7}{12}$,
∴ER=6k=$\frac{7}{2}$.
故答案为$\frac{7}{2}$.
点评 本题考查了相似三角形的判定和性质,菱形的性质,比例的性质,熟练掌握相似三角形的判定和性质定理是解题的关键.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
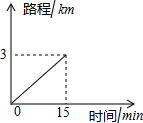 小丽家离学校2km,步行到校需30min,小丽的同学小军上学要经过小丽家,小军骑车上学行驶的路程与时间的关系如图所示.
小丽家离学校2km,步行到校需30min,小丽的同学小军上学要经过小丽家,小军骑车上学行驶的路程与时间的关系如图所示.  已知,如图,在△ABC中,AB=AC,AD是高,DE⊥AB,DF⊥AC,求证:DE=DF.
已知,如图,在△ABC中,AB=AC,AD是高,DE⊥AB,DF⊥AC,求证:DE=DF. 如图,相邻两线段互相垂直,两只蜗牛均同时从A点出发爬往C点,蜗牛甲沿着“A→B→C”路线走,蜗牛乙沿着“A→D→E→F→G→H→I→J→C”的路线走,若他们的爬行速度相同,则先到达点C的是( )
如图,相邻两线段互相垂直,两只蜗牛均同时从A点出发爬往C点,蜗牛甲沿着“A→B→C”路线走,蜗牛乙沿着“A→D→E→F→G→H→I→J→C”的路线走,若他们的爬行速度相同,则先到达点C的是( )