题目内容
6.已知方程2x2-4mx+3(m2-1)=0.求m为何值时,(1)方程有两个正根?
(2)两根异号?
(3)有一个根为0?
分析 (1)直接利用根与系数的关系得出关于m的不等式进而求出即可;
(2)利用根与系数的关系以及根的判别式得出关于m的不等式进而求出即可;
(3)把x=0代入方程求解即可.
解答 解:(1)当方程2x2-4mx+3(m2-1)=0方程有两个正根,
∴$\left\{\begin{array}{l}{-\frac{-4m}{2}>0}\\{\frac{3({m}^{2}-1)}{2}>0}\end{array}\right.$,
解得:m>1,
∴当m>1时,方程2x2-4mx+3(m2-1)=0方程有两个正根;
(2)当方程2x2-4mx+3(m2-1)=0方程有两根异号,
∴$\left\{\begin{array}{l}{(-4m)^{2}-4×2×3({m}^{2}-1)>0}\\{\frac{3({m}^{2}-1)}{2}<0}\end{array}\right.$,
解得:-1<m<1,
∴当-1<m<1时,方程2x2-4mx+3(m2-1)=0方程有两根异号;
(3)当方程2x2-4mx+3(m2-1)=0方程有一个根为0,
∴把x=0代入2x2-4mx+3(m2-1)=0得3(m2-1)=0,
解得:m=±1,
∴当m=±1,方程2x2-4mx+3(m2-1)=0方程有一个根为0.
点评 本题考查的知识点是一元二次方程根与系数的关系以及根的判别式等知识,其中由韦达定理(一元二次方程根与系数的关系)结合已知,构造出关于m的不等式组是解答本题的关键.

练习册系列答案
相关题目
11.下列式子中是二次根式的是( )
| A. | $\sqrt{7}$ | B. | $\root{3}{7}$ | C. | $\sqrt{x}$ | D. | $\sqrt{-7}$ |
15.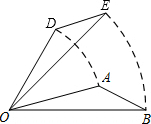 如图,将△AOB绕点O逆时针旋转45°后得到△DOE,若AOB=15°,则∠AOE的度数是( )
如图,将△AOB绕点O逆时针旋转45°后得到△DOE,若AOB=15°,则∠AOE的度数是( )
 如图,将△AOB绕点O逆时针旋转45°后得到△DOE,若AOB=15°,则∠AOE的度数是( )
如图,将△AOB绕点O逆时针旋转45°后得到△DOE,若AOB=15°,则∠AOE的度数是( )| A. | 25° | B. | 30° | C. | 35° | D. | 40° |
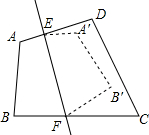 如图,四边形ABCD沿直线EF对着,点A、B的对应点A′,B′落在四边形内部,若∠C+∠D=160°,则∠DEA′+∠CFB′的度数是40°.
如图,四边形ABCD沿直线EF对着,点A、B的对应点A′,B′落在四边形内部,若∠C+∠D=160°,则∠DEA′+∠CFB′的度数是40°. 如图,已知四边形PQRS是菱形,PE=7,EF=6,PF=5,则ER=$\frac{7}{2}$.
如图,已知四边形PQRS是菱形,PE=7,EF=6,PF=5,则ER=$\frac{7}{2}$.