题目内容
10.化简:($\frac{2{x}^{2}+2x}{{x}^{2}-1}$-$\frac{{x}^{2}-x}{{x}^{2}-2x+1}$)÷$\frac{x}{x+1}$,并解答:(1)当x=2时,求原式的值;
(2)原式的值能等于-1吗?为什么?
分析 (1)先根据分式混合运算的法则把原式进行化简,再把x=2代入进行计算即可;
(2)令(1)中的化简结果等于-1,求出x的值即可.
解答 解:(1)原式=[$\frac{2x(x+1)}{(x+1)(x-1)}$-$\frac{x(x-1)}{(x-1)^{2}}$]•$\frac{x+1}{x}$
=[$\frac{2x}{x-1}$-$\frac{x}{x-1}$]•$\frac{x+1}{x}$
=$\frac{x}{x-1}$•$\frac{x+1}{x}$
=$\frac{x+1}{x-1}$,
当x=2时,原式=3;
(2)若原式的值为-1,即$\frac{x+1}{x-1}$=-1,
去分母得:x+1=-x+1,
解得:x=0,…(7分)
代入原式检验,分母为0,不合题意,
则原式的值不可能为-1.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.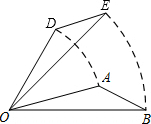 如图,将△AOB绕点O逆时针旋转45°后得到△DOE,若AOB=15°,则∠AOE的度数是( )
如图,将△AOB绕点O逆时针旋转45°后得到△DOE,若AOB=15°,则∠AOE的度数是( )
 如图,将△AOB绕点O逆时针旋转45°后得到△DOE,若AOB=15°,则∠AOE的度数是( )
如图,将△AOB绕点O逆时针旋转45°后得到△DOE,若AOB=15°,则∠AOE的度数是( )| A. | 25° | B. | 30° | C. | 35° | D. | 40° |
19.若x2+2(2p-3)x+4是完全平方式,则p的值等于( )
| A. | $\frac{5}{2}$ | B. | 2 | C. | 2或1 | D. | $\frac{5}{2}$或$\frac{1}{2}$ |
20.下列计算正确的是( )
| A. | a•a=a2 | B. | a3+a3=a6 | C. | a4•a2=a8 | D. | (a3)2=a9 |
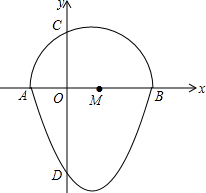 我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,AB为半圆的直径,点M为圆心,A点坐标为(-2,0),B点坐标为(4,0),D点的坐标为(0,-4).
我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,AB为半圆的直径,点M为圆心,A点坐标为(-2,0),B点坐标为(4,0),D点的坐标为(0,-4). 如图,已知四边形PQRS是菱形,PE=7,EF=6,PF=5,则ER=$\frac{7}{2}$.
如图,已知四边形PQRS是菱形,PE=7,EF=6,PF=5,则ER=$\frac{7}{2}$.
 如图所示,正方形网格中,ABC为格点三角形(即三角形的顶点都在格点上).
如图所示,正方形网格中,ABC为格点三角形(即三角形的顶点都在格点上).