题目内容
9．分解因式：（c2-b2+d2-a2）2-4（ab-cd）2=（c-d+a-b）（c-d-a+b）（c+d+a+b）（c+d-a-b）．分析 原式利用平方差公式化简，再利用完全平方公式及平方差公式分解即可．
解答 解：原式=（c2-b2+d2-a2+2ab-2cd）（c2-b2+d2-a2-2ab+2cd）
=[（c-d）2-（a-b）2][（c+d）2-（a+b）2]
=（c-d+a-b）（c-d-a+b）（c+d+a+b）（c+d-a-b）．
故答案为：（c-d+a-b）（c-d-a+b）（c+d+a+b）（c+d-a-b）
点评 此题考查了因式分解-运用公式法，熟练掌握完全平方公式及平方差公式是解本题的关键．
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
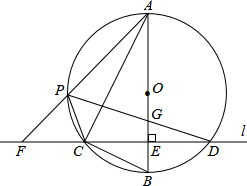如图，在⊙O的内接△ABC中，∠ACB=90°，tan∠CAB=$\frac{1}{2}$，过C作AB的垂线l交⊙O于另一点D，垂足为E．设P是$\widehat{AC}$上异于A，C的一个动点，射线AP交l于点F，连接PC与PD，PD交AB于点G．
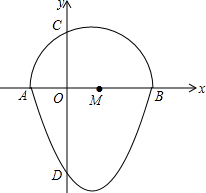我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”，如果一条直线与“蛋圆”只有一个交点，那么这条直线叫做“蛋圆”的切线．如图，点A、B、C、D分别是“蛋圆”与坐标轴的交点，AB为半圆的直径，点M为圆心，A点坐标为（-2，0），B点坐标为（4，0），D点的坐标为（0，-4）．
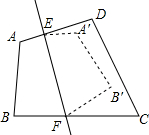如图，四边形ABCD沿直线EF对着，点A、B的对应点A′，B′落在四边形内部，若∠C+∠D=160°，则∠DEA′+∠CFB′的度数是40°．
如图，已知四边形PQRS是菱形，PE=7，EF=6，PF=5，则ER=$\frac{7}{2}$．
19．若x2+2（2p-3）x+4是完全平方式，则p的值等于（ ）
| A． | $\frac{5}{2}$ | B． | 2 | C． | 2或1 | D． | $\frac{5}{2}$或$\frac{1}{2}$ |