题目内容
观察下列各等式,并回答问题:
=1-
;
=
-
;
=
-
;
=
-
;…
(1)填空:
= (n是正整数)
(2)计算:
+
+
+
+…+
= .
(3)若|ab-3|与|b-1|互为相反数,求
+
+
+
…+
的值.
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4×5 |
| 1 |
| 4 |
| 1 |
| 5 |
(1)填空:
| 1 |
| n(n+1) |
(2)计算:
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 4×5 |
| 1 |
| 2004×2005 |
(3)若|ab-3|与|b-1|互为相反数,求
| 1 |
| ab |
| 1 |
| (a+2)(b+2) |
| 1 |
| (a+4)(b+4) |
| 1 |
| (a+6)(b+6) |
…+
| 1 |
| (a+2010)(b+2010) |
考点:有理数的混合运算
专题:规律型
分析:(1)将分式进行拆项即可求解;
(2)先拆项,再抵消即可求解;
(3)先根据非负数的性质得到a、b的值,再拆项抵消即可求解.
(2)先拆项,再抵消即可求解;
(3)先根据非负数的性质得到a、b的值,再拆项抵消即可求解.
解答:解:(1)
=
-
;
(2)
+
+
+
+…+
=1-
+
-
+…+
-
=1-
=
;
(3)∵|ab-3|与|b-1|互为相反数,
∴|ab-3|+|b-1|=0,
∴ab-3=0,b-1=0,
解得a=3,b=1,
∴
+
+
+
+…+
=
×(1-
)
=
×
=
.
故答案为:
-
;
.
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
(2)
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 4×5 |
| 1 |
| 2004×2005 |
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2004 |
| 1 |
| 2005 |
=1-
| 1 |
| 2005 |
=
| 2004 |
| 2005 |
(3)∵|ab-3|与|b-1|互为相反数,
∴|ab-3|+|b-1|=0,
∴ab-3=0,b-1=0,
解得a=3,b=1,
∴
| 1 |
| ab |
| 1 |
| (a+2)(b+2) |
| 1 |
| (a+4)(b+4) |
| 1 |
| (a+6)(b+6) |
| 1 |
| (a+2010)(b+2010) |
=
| 1 |
| 2 |
| 1 |
| 2013 |
=
| 1 |
| 2 |
| 2012 |
| 2013 |
=
| 1006 |
| 2013 |
故答案为:
| 1 |
| n |
| 1 |
| n+1 |
| 2004 |
| 2005 |
点评:考查了有理数的混合运算,本题关键是熟练运用
=
-
.
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
在△ABC中,AB=12cm,BC=16cm,AC=20cm,则S△ABC为( )
| A、96cm2 |
| B、120cm2 |
| C、160cm2 |
| D、200cm2 |
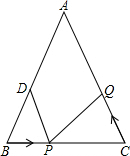 如图,已知△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB 的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动.当一个点停止运动时时,另一个点也随之停止运动.设运动时间为t.
如图,已知△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB 的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动.当一个点停止运动时时,另一个点也随之停止运动.设运动时间为t.