题目内容
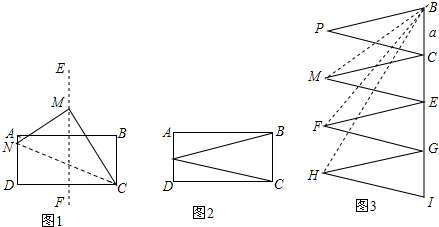
2.已知,矩形ABCD.(1)如图1把矩形ABCD对折,使AD与BC重合(即A点与B点重合,D点与C点重合),得到折痕EF,展开后再一次过点C折叠纸片,使D点落在直线EF上,记为点M(折痕为CN),求∠MNC的度数.
(2)如图2,取AD边的中点P,剪下△BPC,将△BPC沿着射线BC的方向依次进行平移变换,每次均移动BC的长度,得到△CME,△EFG和△GHI(如图3).若BH=BI,BC=a.
①连接BM,BF,BH,证明BM,BF,BH为三边构成的新三角形是直角三角形;
②若这个新三角形面积小于50$\sqrt{15}$,直接写出a的最大整数值.
分析 (1)利用线段垂直平分线的性质结合翻折变换的性质得出△MDC为等边三角形,进而得出∠MNC的度数;
(2)①分别取CE、EG、GI的中点R、Q、N,连接RM、FQ、HN、BM、BF、BH,由BP=PC,根据平移变换的性质,就有△CME、△EFG和△GHI都是等腰三角形,就有RM⊥CE,FQ⊥EG,HN⊥GI,由勾股定理就可以求出HN2=$\frac{15}{4}$a2,从而得出新三角形三边的值,从而得出结论;
②利用直角三角形面积求法结合二次根式的性质得出答案.
解答  解:(1)如答图1,连接DM,
解:(1)如答图1,连接DM,
由题意得EF垂直平分DC,故MC=DM,由翻折可得,DC=MC,∠1=∠2,
故△MDC为等边三角形,
∴∠MCD=60°,
∴∠1=∠2=30°,
∴∠MNC=60°;
(2)①如答图2,分别取CE、EG、GI的中点R、Q、N,连接RM、FQ、HN、BM、BF、BH,
∵△PBC中,PB=PC,根据平移变换的性质,△CME、△EFG和△GHI都是等腰三角形,
∴RM⊥CE,FQ⊥EG,HN⊥GI.
在Rt△BHN中,BH=BI=4a,
BH2=HN2+BN2,HN2=$\frac{15}{4}$a2,
则RM2=FQ2=HN2=$\frac{15}{4}$a2,
BM2=BR2+RM2=6a2,BF2=BQ2+FQ2=10a2,
新三角形三边长为4a、$\sqrt{6}$a、$\sqrt{10}$a.
∵BH2=BM2+BF2
∴新三角形为直角三角形.
(或通过转换得新三角形三边就是BM、MI、BI,即求△BMI的面积或利用△HBI与△HGI相似,求△HBI的面积也可以).
②由①得:新三角形为直角三角形,其面积为:
$\frac{1}{2}$×BM×BF=$\frac{1}{2}$$\sqrt{6}$a•$\sqrt{10}$a=$\sqrt{15}$a2.
∵这个新三角形面积小于50$\sqrt{15}$,
∴$\sqrt{15}$a2<50$\sqrt{15}$,
∴a2<50
∴a的最大整数值为7.
点评 本题考查了翻折变换的运用、平移变换的运用、勾股定理的运用,等腰三角形的性质的运用、三角形的面积公式的运用.本题的综合性较强要求学生熟练的运用图形变换解题是关键.

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | $\frac{3}{4}$,4 | B. | $\frac{3}{4}$,2 | C. | $\frac{3π}{4}$,3 | D. | $\frac{3π}{4}$,2 |
 已知等边三角形ABC的边长为2,将这个三角形放置在如图所示的直角坐标系中,且B,C两点的坐标分别为(-1,0),(1,0)
已知等边三角形ABC的边长为2,将这个三角形放置在如图所示的直角坐标系中,且B,C两点的坐标分别为(-1,0),(1,0)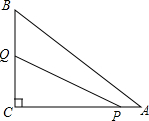 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点P从点A出发,沿AC以每秒1个单位的速度向终点C运动,点Q从点C出发,沿C-B-A以每秒2个单位的速度向终点A运动,当点P停止运动时,点Q也随之停止,点P,Q同时出发,设点P的运动时间为t(秒).
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点P从点A出发,沿AC以每秒1个单位的速度向终点C运动,点Q从点C出发,沿C-B-A以每秒2个单位的速度向终点A运动,当点P停止运动时,点Q也随之停止,点P,Q同时出发,设点P的运动时间为t(秒).