题目内容
20. 已知等边三角形ABC的边长为2,将这个三角形放置在如图所示的直角坐标系中,且B,C两点的坐标分别为(-1,0),(1,0)
已知等边三角形ABC的边长为2,将这个三角形放置在如图所示的直角坐标系中,且B,C两点的坐标分别为(-1,0),(1,0)(1)在图中画出△ABC;
(2)求点A的坐标;
(3)把△ABC向右平移4个单位,求△ABC扫过的面积.
分析 (1)根据题意画出△ABC即可,有两种情况;
(2)由勾股定理求出OA,即可得出结果;
(3)根据题意得出△ABC扫过的图形是一个平行四边形,由平行四边形的面积公式即可得出结果.
解答 解:(1)△ABC如图所示: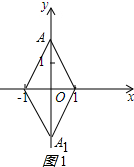
(2)由勾股定理得:OA=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴点A的坐标为(0,$\sqrt{3}$),或(0,-$\sqrt{3}$);
(3)∵把△ABC向右平移4个单位,
∴△ABC扫过的图形是一个平行四边形,
如图2所示:
平行四边形的一条边为4,这边上的高为$\sqrt{3}$,
∴△ABC扫过的面积=4×$\sqrt{3}$=4$\sqrt{3}$.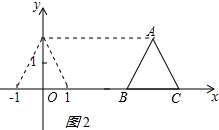
点评 本题考查了等边三角形的性质、坐标与图形性质、平移的性质;熟练掌握等边三角形的性质是解决问题的关键,注意分类讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
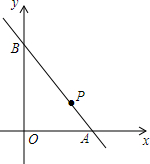 如图,直线y=-$\frac{3}{4}$x+3与x轴,y轴分别交于A、B两点,点P是线段AB的动点,若使得△OAP为等腰三角形,求点P的坐标.
如图,直线y=-$\frac{3}{4}$x+3与x轴,y轴分别交于A、B两点,点P是线段AB的动点,若使得△OAP为等腰三角形,求点P的坐标.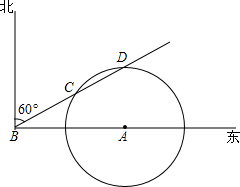 如图,在气象站台A的正西方向320km的B处有一台风中心,该台风中心以每小时20km的速度沿北偏东60°的BD方向移动,在距离台风中心200km内的地方都要受到其影响.
如图,在气象站台A的正西方向320km的B处有一台风中心,该台风中心以每小时20km的速度沿北偏东60°的BD方向移动,在距离台风中心200km内的地方都要受到其影响.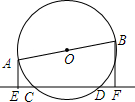 圆O的直径AB=10cm,CD长是圆O的$\frac{1}{6}$,AE⊥CD于E,BF⊥CD于F.
圆O的直径AB=10cm,CD长是圆O的$\frac{1}{6}$,AE⊥CD于E,BF⊥CD于F.