题目内容
 如图,一次函数y=kx+b的图象l与坐标轴分别交于点E、F,与双曲线y=-
如图,一次函数y=kx+b的图象l与坐标轴分别交于点E、F,与双曲线y=-| 4 |
| x |
(1)求直线l的解析式;
(2)若直线x=a与l交于点A,与双曲线交于点B(不同于A),问a为何值时,PA=PB?
考点:反比例函数与一次函数的交点问题
专题:数形结合
分析:(1)先由y=-
,求出点P的坐标,再根据F为PE中点,求出F的坐标,把P,F的坐标代入求出直线l的解析式;
(2)过P作PD⊥AB,垂足为点D,由A点的纵坐标为-2a+2,B点的纵坐标为-
,D点的纵坐标为4,列出方程求解即可.
| 4 |
| x |
(2)过P作PD⊥AB,垂足为点D,由A点的纵坐标为-2a+2,B点的纵坐标为-
| 4 |
| a |
解答:解:由P(-1,n)在y=-
上,得n=4,
∴P(-1,4),
∵F为PE中点,
∴OF=
n=2,
∴F(0,2),
又∵P,F在y=kx+b上,
∴
,
解得
.
∴直线l的解析式为:y=-2x+2.
(2)如图,过P作PD⊥AB,垂足为点D,

∵PA=PB,
∴点D为AB的中点,
又由题意知A点的纵坐标为-2a+2,B点的纵坐标为-
,D点的纵坐标为4,
∴得方程-2a+2-
=4×2,
解得a1=-2,a2=-1(舍去).
∴当a=-2时,PA=PB.
| 4 |
| x |
∴P(-1,4),
∵F为PE中点,
∴OF=
| 1 |
| 2 |
∴F(0,2),
又∵P,F在y=kx+b上,
∴
|
解得
|
∴直线l的解析式为:y=-2x+2.
(2)如图,过P作PD⊥AB,垂足为点D,

∵PA=PB,
∴点D为AB的中点,
又由题意知A点的纵坐标为-2a+2,B点的纵坐标为-
| 4 |
| a |
∴得方程-2a+2-
| 4 |
| a |
解得a1=-2,a2=-1(舍去).
∴当a=-2时,PA=PB.
点评:本题主要考查了反比例函数与一次函数的交点,解题的重点是求出直线l的解析式.

练习册系列答案
相关题目
某校九年级8位同学一分钟跳绳的次数排序后如下:150,164,168,168,172,176,183,185.则由这组数据得到的结论中错误的是( )
| A、中位数为170 |
| B、众数为168 |
| C、极差为35 |
| D、平均数为171 |
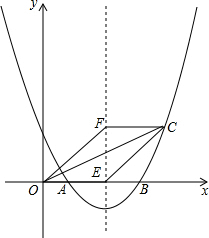 如图,抛物线y=ax2+bx+2与x轴交于点A(1,0)和B(4,0).
如图,抛物线y=ax2+bx+2与x轴交于点A(1,0)和B(4,0). 在△ABC中,有两点E、F分别在边AB、AC的延长线上,连接EF,且EF∥BC,5AB=8AC,AF=3,求AE的长.
在△ABC中,有两点E、F分别在边AB、AC的延长线上,连接EF,且EF∥BC,5AB=8AC,AF=3,求AE的长. 如图,D是△ABC的边AC上的一点,连接BD,已知∠ABD=∠C,AB=6,AD=4,求线段CD的长.
如图,D是△ABC的边AC上的一点,连接BD,已知∠ABD=∠C,AB=6,AD=4,求线段CD的长. 如图,△ABC中,∠A=60°,将△ABC沿DE翻折后,点A落在BC边上的点A′处.如果∠A′EC=70°,那么∠A′DE的度数为
如图,△ABC中,∠A=60°,将△ABC沿DE翻折后,点A落在BC边上的点A′处.如果∠A′EC=70°,那么∠A′DE的度数为