题目内容
20.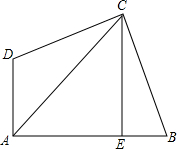 如图:AC平分∠BAD,CE⊥AB,∠B与∠D互补.求证:AE=AD+BE(提示:在AE上取F,使EF=EB,连接CF.)
如图:AC平分∠BAD,CE⊥AB,∠B与∠D互补.求证:AE=AD+BE(提示:在AE上取F,使EF=EB,连接CF.)
分析 在AE上取F,使EF=EB,连接CF,证得△CEF≌△CEB和△ADC≌△AFC,得出相应的角和线段相等,证得结论成立即可.
解答 证明:如图,
在AE上取F,使EF=EB,连接CF.
∵CE⊥AB,
∴∠CEF=∠CEB=90°,
在△CEF和△CEB中,
$\left\{\begin{array}{l}{CE=CE}\\{∠CEF=∠CEB}\\{EF=EB}\end{array}\right.$,
∴△CEF≌△CEB,
∴∠CFE=∠B,
∵∠B+∠D=180°,
∴∠CFA=180°-∠CFE=∠D
∵AC平分∠BAD,
∴∠DAC=∠FAC,
在△ADC和△AFC中,
$\left\{\begin{array}{l}{∠CAD=∠CAF}\\{∠CDA=∠CFA}\\{AC=AC}\end{array}\right.$,
∴△ADC≌△AFC,
∴AD=AF,
∴AE=AF+FE=AD+BE.
点评 此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
12.在△ABC中,∠A=50°,O为△ABC的内心,则∠BOC的度数是( )
| A. | 115° | B. | 65° | C. | 130° | D. | 155° |
9.若-$\sqrt{5}$$<x<\sqrt{3}$,且x是整数,则满足条件的x值有( )
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
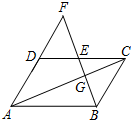 如图,?ABCD中,E是边CD的中点,连结BE并延长,交AD的延长线于点F.
如图,?ABCD中,E是边CD的中点,连结BE并延长,交AD的延长线于点F. 如图,四边形ABCD是矩形,AE∥BD交CD延长线于E.试说明:AC=AE.
如图,四边形ABCD是矩形,AE∥BD交CD延长线于E.试说明:AC=AE.