题目内容
11.解方程组:(1)用加减法 $\left\{\begin{array}{l}2x-3y=0\\ x+2y=3\end{array}\right.$
(2)$\left\{\begin{array}{l}\frac{x}{2}+\frac{y}{3}=\frac{13}{2}\\ \frac{x}{3}-\frac{y}{4}=\frac{3}{2}\end{array}\right.$.
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{2x-3y=0①}\\{x+2y=3②}\end{array}\right.$,
②×2-①得:7y=6,即y=$\frac{6}{7}$,
把y=$\frac{6}{7}$代入①得:x=$\frac{9}{7}$,
则方程组的解为$\left\{\begin{array}{l}x=\frac{9}{7}\\ y=\frac{6}{7}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{3x+2y=39①}\\{4x-3y=18②}\end{array}\right.$,
①×3+②×2得:17x=153,即x=9,
把x=9代入①得:y=6,
则方程组的解为$\left\{\begin{array}{l}x=9\\ y=6\end{array}\right.$.
点评 此题考查了解二元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
2. 某种零件模型如图所示,该几何体(空心圆柱)的主视图是( )
某种零件模型如图所示,该几何体(空心圆柱)的主视图是( )
 某种零件模型如图所示,该几何体(空心圆柱)的主视图是( )
某种零件模型如图所示,该几何体(空心圆柱)的主视图是( )| A. |  | B. |  | C. |  | D. |  |
19.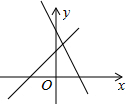 如图,一次函数y1=ax+b和y2=-bx+a(a≠0,b≠0)在同一坐标系的图象.则$\left\{\begin{array}{l}{y_1}=ax+b\\{y_2}=-bx+a\end{array}\right.$的解$\left\{\begin{array}{l}x=m\\ y=n\end{array}\right.$中( )
如图,一次函数y1=ax+b和y2=-bx+a(a≠0,b≠0)在同一坐标系的图象.则$\left\{\begin{array}{l}{y_1}=ax+b\\{y_2}=-bx+a\end{array}\right.$的解$\left\{\begin{array}{l}x=m\\ y=n\end{array}\right.$中( )
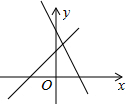 如图,一次函数y1=ax+b和y2=-bx+a(a≠0,b≠0)在同一坐标系的图象.则$\left\{\begin{array}{l}{y_1}=ax+b\\{y_2}=-bx+a\end{array}\right.$的解$\left\{\begin{array}{l}x=m\\ y=n\end{array}\right.$中( )
如图,一次函数y1=ax+b和y2=-bx+a(a≠0,b≠0)在同一坐标系的图象.则$\left\{\begin{array}{l}{y_1}=ax+b\\{y_2}=-bx+a\end{array}\right.$的解$\left\{\begin{array}{l}x=m\\ y=n\end{array}\right.$中( )| A. | m>0,n>0 | B. | m>0,n<0 | C. | m<0,n>0 | D. | m<0,n<0 |
6.下列图形中内角和等于360°的是( )
| A. | 三角形 | B. | 四边形 | C. | 五边形 | D. | 六边形 |
16.某工厂计划生产A、B两种产品共10件,其生产成本和利润如下表:
(1)若工厂计划获利14万元,问A、B两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于35万元,且获利多于14万元,问工厂有哪几种生产方案?
(3)在(2)的条件下,哪种生产方案获利最大?并求出最大利润.
| A种产品 | B种产品 | |
| 成本(万元/件) | 2 | 5 |
| 利润(万元/件) | 1 | 3 |
(2)若工厂计划投入资金不多于35万元,且获利多于14万元,问工厂有哪几种生产方案?
(3)在(2)的条件下,哪种生产方案获利最大?并求出最大利润.
1.若a≤0,则|a|+a+2等于( )
| A. | 2a+2 | B. | 2 | C. | 2-2a | D. | 2a-2 |
 如图,在圆内接四边形ABCD中,若∠A=60°,则∠C的大小为120°.
如图,在圆内接四边形ABCD中,若∠A=60°,则∠C的大小为120°.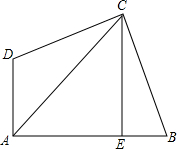 如图:AC平分∠BAD,CE⊥AB,∠B与∠D互补.求证:AE=AD+BE(提示:在AE上取F,使EF=EB,连接CF.)
如图:AC平分∠BAD,CE⊥AB,∠B与∠D互补.求证:AE=AD+BE(提示:在AE上取F,使EF=EB,连接CF.)