题目内容
10.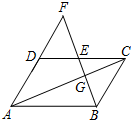 如图,?ABCD中,E是边CD的中点,连结BE并延长,交AD的延长线于点F.
如图,?ABCD中,E是边CD的中点,连结BE并延长,交AD的延长线于点F.(1)求证:EF=EB;
(2)连结AC,交BF于点G,若EG=2,求EF的长.
分析 (1)根据平行四边形的性质得出AB∥DF,推出∠ABE=∠F,根据全等三角形的判定定理推出△CBE≌△DFE,然后由全等三角形的性质即可得到结论;
(2)根据相似三角形的性质得到$\frac{BG}{EG}=\frac{AB}{CE}=2$,求得BG=2EG=4,得到BE=6,即可得到结论.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴CB∥DF,
∴∠CBE=∠F,
∵点E是AD的中点,
∴AE=DE,
在△CBE和△DFE中
$\left\{\begin{array}{l}{∠CEB=∠DEF}\\{∠CBE=∠F}\\{CE=DE}\end{array}\right.$
∴△CBE≌△DFE,
∴BE=EF;
(2)∵AB∥CD,
∴△CEG∽△ABG,
∴$\frac{BG}{EG}=\frac{AB}{CE}=2$,
∴BG=2EG=4,
∴BE=6,
∴EF=BG=6.
点评 本题考查了全等三角形的判定和性质,平行四边形的性质,相似三角形的判定和性质,解此题的关键是推出∠CBE=∠F.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
5.学校举行红歌赛,全校21个班级均组队参赛.所有参赛代表队的成绩互不相同,小敏在已知自己班级代表队成绩的情况下,要想知道本班代表队是否进入前10名,只需要知道所有参赛代表队成绩的( )
| A. | 平均数 | B. | 众数 | C. | 中位数 | D. | 方差 |
2. 某种零件模型如图所示,该几何体(空心圆柱)的主视图是( )
某种零件模型如图所示,该几何体(空心圆柱)的主视图是( )
 某种零件模型如图所示,该几何体(空心圆柱)的主视图是( )
某种零件模型如图所示,该几何体(空心圆柱)的主视图是( )| A. |  | B. |  | C. |  | D. |  |
 如图,在圆内接四边形ABCD中,若∠A=60°,则∠C的大小为120°.
如图,在圆内接四边形ABCD中,若∠A=60°,则∠C的大小为120°. 有四张背面相同的扑克牌,正面图形如下.小明摸两次,每次在洗牌后均摸一张.两次均摸出中心对称的图形的概率是多少?(用表格或树状图分析)
有四张背面相同的扑克牌,正面图形如下.小明摸两次,每次在洗牌后均摸一张.两次均摸出中心对称的图形的概率是多少?(用表格或树状图分析) 如图,直角三角形斜边长为12,内切圆的半径为1,求三角形的周长.
如图,直角三角形斜边长为12,内切圆的半径为1,求三角形的周长.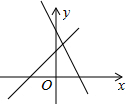 如图,一次函数y1=ax+b和y2=-bx+a(a≠0,b≠0)在同一坐标系的图象.则$\left\{\begin{array}{l}{y_1}=ax+b\\{y_2}=-bx+a\end{array}\right.$的解$\left\{\begin{array}{l}x=m\\ y=n\end{array}\right.$中( )
如图,一次函数y1=ax+b和y2=-bx+a(a≠0,b≠0)在同一坐标系的图象.则$\left\{\begin{array}{l}{y_1}=ax+b\\{y_2}=-bx+a\end{array}\right.$的解$\left\{\begin{array}{l}x=m\\ y=n\end{array}\right.$中( )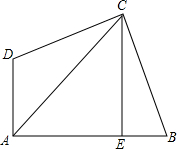 如图:AC平分∠BAD,CE⊥AB,∠B与∠D互补.求证:AE=AD+BE(提示:在AE上取F,使EF=EB,连接CF.)
如图:AC平分∠BAD,CE⊥AB,∠B与∠D互补.求证:AE=AD+BE(提示:在AE上取F,使EF=EB,连接CF.)