题目内容
12.在△ABC中,∠A=50°,O为△ABC的内心,则∠BOC的度数是( )| A. | 115° | B. | 65° | C. | 130° | D. | 155° |
分析 由三角形的内角和定理可知∠ABC+∠ACB=130°,从而可求得∠OBC+∠OCB=65°,最后利用三角形的内角和定理可求得∠BOC=115°.
解答 解:如图所示: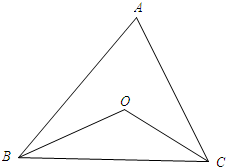
∵∠A=50°,
∴∠ABC+∠ACB=130°.
∵O为△ABC的内心,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB.
∴∠OBC+OCB=$\frac{1}{2}$×130°=65°.
∴∠BOC=180°-65°=115°.
故选:A.
点评 本题主要考查的是三角形的内心,根据三角形内心的特点得到∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB是解题的关键.

练习册系列答案
相关题目
2. 某种零件模型如图所示,该几何体(空心圆柱)的主视图是( )
某种零件模型如图所示,该几何体(空心圆柱)的主视图是( )
 某种零件模型如图所示,该几何体(空心圆柱)的主视图是( )
某种零件模型如图所示,该几何体(空心圆柱)的主视图是( )| A. |  | B. |  | C. |  | D. |  |
4.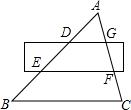 如图,△ABC被一平行于BC的矩形所截,AB被截成三等分,若△ADG的面积为a,则图中四边形DEFG的面积是( )
如图,△ABC被一平行于BC的矩形所截,AB被截成三等分,若△ADG的面积为a,则图中四边形DEFG的面积是( )
 如图,△ABC被一平行于BC的矩形所截,AB被截成三等分,若△ADG的面积为a,则图中四边形DEFG的面积是( )
如图,△ABC被一平行于BC的矩形所截,AB被截成三等分,若△ADG的面积为a,则图中四边形DEFG的面积是( )| A. | a | B. | 2a | C. | 3a | D. | 4a |
1.若a≤0,则|a|+a+2等于( )
| A. | 2a+2 | B. | 2 | C. | 2-2a | D. | 2a-2 |
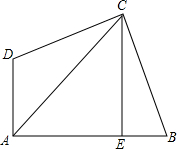 如图:AC平分∠BAD,CE⊥AB,∠B与∠D互补.求证:AE=AD+BE(提示:在AE上取F,使EF=EB,连接CF.)
如图:AC平分∠BAD,CE⊥AB,∠B与∠D互补.求证:AE=AD+BE(提示:在AE上取F,使EF=EB,连接CF.) 如图,已知Rt△ABC≌Rt△DEC,连结AD,若∠1=25°,则∠B的度数是70°.
如图,已知Rt△ABC≌Rt△DEC,连结AD,若∠1=25°,则∠B的度数是70°.