题目内容
2.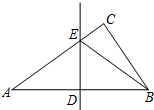 如图,在Rt△ABC中,∠ACB=90°,DE是AB的中垂线,分别交AB,AC于点D,E.已知AB=13,AC=12,则△BCE的周长是17.
如图,在Rt△ABC中,∠ACB=90°,DE是AB的中垂线,分别交AB,AC于点D,E.已知AB=13,AC=12,则△BCE的周长是17.
分析 由在Rt△ABC中,∠ACB=90°,AB=13,AC=12,利用勾股定理即可求得BC的长,然后由DE是AB的中垂线,根据线段垂直平分线的性质,可得AE=BE,继而可得△BCE的周长=AC+BC.
解答 解:∵在Rt△ABC中,∠ACB=90°,AB=13,AC=12,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=5,
∵DE是AB的中垂线,
∴AE=BE,
∴△BCE的周长是:BC+CE+BE=BC+CE+AE=BC+AC=17.
故答案为:17.
点评 此题考查了线段垂直平分线的性质以及勾股定理.注意垂直平分线上任意一点,到线段两端点的距离相等.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
12.已知a-b≠0,且2a-3b=0,则$\frac{2a+b}{a-b}$的值是( )
| A. | -12 | B. | 0 | C. | 8 | D. | 8或12 |
14.下列说法正确的是( )
| A. | x3yz没有系数,次数是5 | B. | 3x-4y+6z2不是单项式,也不是整式 | ||
| C. | a+$\frac{a}{b}$是多项式 | D. | x2y+2是三次二项式 |
 如图,抛物线y=-$\frac{1}{3}{x}^{2}$+2x与x轴相交于点B、O,点A是抛物线的顶点,连接AB,把AB所在的直线平移,使它经过原点O,得到直线l.已知点P是直线l上的一点,且它在x轴的上方.设以点A、B、O、P为顶点的四边形面积为S,点P的横坐标为t.当12≤S≤18时,t的取值范围是-3≤t≤-1.
如图,抛物线y=-$\frac{1}{3}{x}^{2}$+2x与x轴相交于点B、O,点A是抛物线的顶点,连接AB,把AB所在的直线平移,使它经过原点O,得到直线l.已知点P是直线l上的一点,且它在x轴的上方.设以点A、B、O、P为顶点的四边形面积为S,点P的横坐标为t.当12≤S≤18时,t的取值范围是-3≤t≤-1.