题目内容
11.一个三位数M,百位数字为a,十位数字为b,个位数字是c.(1)请用含a,b,c的式子表示这个数M;
(2)现在交换百位数字和个位数字,得到一个新的三位数N,请用含a,b,c的式子表示N;
(3)请用含a,b,c的式子表示N-M,并回答N-M能被11整除吗?
分析 (1)根据百位数字为a,十位数字为b,个位数字是c表示出M即可;
(2)同(1)可表示出N;
(3)列出整式相加减的式子,再合并同类项即可.
解答 解:(1)M为:100a+10b+c;
(2)N为:100c+10b+a;
(3)∵N-M=(100c+10b+a)-(100a+10b+c)
=99c-99a
=99(c-a).
∴N-M能被11整除.
点评 本题考查的是整式的加减,熟知整式的加减实质上就是合并同类项是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.下列各式正确的是( )
| A. | $\frac{6}{7}$<$\frac{5}{6}$ | B. | -|-5|>-4 | C. | -$\frac{5}{6}$<-$\frac{4}{5}$ | D. | -$\frac{5}{4}$>-1.25 |
3. 如图,BC是⊙O的直径,点D在⊙O上,AB是⊙O的切线,B为切点,连接CD并延长交AB于点A,若∠BOD=100°,则∠BAC的度数是( )
如图,BC是⊙O的直径,点D在⊙O上,AB是⊙O的切线,B为切点,连接CD并延长交AB于点A,若∠BOD=100°,则∠BAC的度数是( )
 如图,BC是⊙O的直径,点D在⊙O上,AB是⊙O的切线,B为切点,连接CD并延长交AB于点A,若∠BOD=100°,则∠BAC的度数是( )
如图,BC是⊙O的直径,点D在⊙O上,AB是⊙O的切线,B为切点,连接CD并延长交AB于点A,若∠BOD=100°,则∠BAC的度数是( )| A. | 40° | B. | 45° | C. | 50° | D. | 80° |
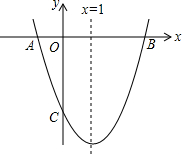 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过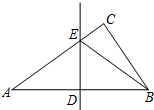 如图,在Rt△ABC中,∠ACB=90°,DE是AB的中垂线,分别交AB,AC于点D,E.已知AB=13,AC=12,则△BCE的周长是17.
如图,在Rt△ABC中,∠ACB=90°,DE是AB的中垂线,分别交AB,AC于点D,E.已知AB=13,AC=12,则△BCE的周长是17.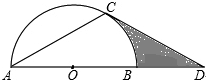 如图,AC是⊙O的弦,AD经过圆心O,交⊙O于点B,直线CD与⊙O相切,∠CAD=30°.
如图,AC是⊙O的弦,AD经过圆心O,交⊙O于点B,直线CD与⊙O相切,∠CAD=30°.