题目内容
17.已知:⊙O中的半径为4cm,弦AB所对的劣弧为圆的$\frac{1}{3}$,则弦AB的长为2cm,AB的弦心距为4$\sqrt{3}$cm.分析 根据弦AB所对的劣弧为圆的$\frac{1}{3}$可得出∠AOB=120°,再由垂径定理可以得到∠AOC=60°,所以∠OAC=30°,根据锐角三角函数的定义可求出AC及OC的长,进而得出结论.
解答  解:如图,
解:如图,
∵弦AB所对的劣弧为圆的$\frac{1}{3}$,
∴∠AOB=$\frac{1}{3}$×360°=120°.
∵OC⊥AB,OA=OB,
∴AC=CB,∠OAC=30°,
∴OC=$\frac{1}{2}$OA=2,AC=OA•sin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∴AB=2AC=4$\sqrt{3}$.
故答案为:2,4$\sqrt{3}$.
点评 本题考查的是垂径定理,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
相关题目
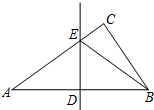 如图,在Rt△ABC中,∠ACB=90°,DE是AB的中垂线,分别交AB,AC于点D,E.已知AB=13,AC=12,则△BCE的周长是17.
如图,在Rt△ABC中,∠ACB=90°,DE是AB的中垂线,分别交AB,AC于点D,E.已知AB=13,AC=12,则△BCE的周长是17.