题目内容
12.已知动点P以每秒2cm的速度沿图甲的边框按从B→C→D→E→F→A的路径移动,相应的△ABP的面积S关于时间t的函数的图象如图乙,若AB=6cm,则图乙中a+b的值为41.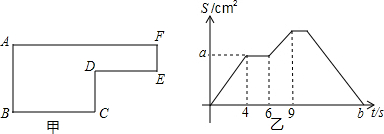
分析 根据题意得:动点P在BC上运动的时间是4秒,又由动点的速度,可得BC的长;又由AB=6cm,可以计算出△ABP的面积,计算可得a的值;计算BC+CD+DE+EF+FA的长度,又由P的速度,计算可得b的值;进一步代入求得答案即可.
解答 解:动点P在BC上运动时,对应的时间为0到4秒,易得:BC=2cm/秒×4秒=8cm;
则a=$\frac{1}{2}$×BC×AB=24cm2;
图乙中的a=24.
由图可得:CD=2×2=4cm,DE=2×3=6cm,
则AF=BC+DE=14cm,又由AB=6cm,
动点P共运动了BC+CD+DE+EF+FA=8+4+6+2+14=34cm,
其速度是2cm/秒,则b=$\frac{34}{2}$=17秒,
图乙中的b=17.
图乙中a+b的值为41.
故答案为:41.
点评 本题考查动点问题的函数图象,解题的关键是读懂图意,明确横轴与纵轴的意义.

练习册系列答案
相关题目
3. 如图,BC是⊙O的直径,点D在⊙O上,AB是⊙O的切线,B为切点,连接CD并延长交AB于点A,若∠BOD=100°,则∠BAC的度数是( )
如图,BC是⊙O的直径,点D在⊙O上,AB是⊙O的切线,B为切点,连接CD并延长交AB于点A,若∠BOD=100°,则∠BAC的度数是( )
 如图,BC是⊙O的直径,点D在⊙O上,AB是⊙O的切线,B为切点,连接CD并延长交AB于点A,若∠BOD=100°,则∠BAC的度数是( )
如图,BC是⊙O的直径,点D在⊙O上,AB是⊙O的切线,B为切点,连接CD并延长交AB于点A,若∠BOD=100°,则∠BAC的度数是( )| A. | 40° | B. | 45° | C. | 50° | D. | 80° |
17.下列各组中,两个单项式是同类项的是( )
| A. | 3mn与-4nm | B. | -mn2与m2n | C. | 2x3与-3y3 | D. | 3ab与-abc |
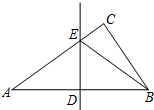 如图,在Rt△ABC中,∠ACB=90°,DE是AB的中垂线,分别交AB,AC于点D,E.已知AB=13,AC=12,则△BCE的周长是17.
如图,在Rt△ABC中,∠ACB=90°,DE是AB的中垂线,分别交AB,AC于点D,E.已知AB=13,AC=12,则△BCE的周长是17.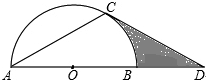 如图,AC是⊙O的弦,AD经过圆心O,交⊙O于点B,直线CD与⊙O相切,∠CAD=30°.
如图,AC是⊙O的弦,AD经过圆心O,交⊙O于点B,直线CD与⊙O相切,∠CAD=30°.