题目内容
分解因式：（x-y）5+（y-x）3．
考点：提公因式法与公式法的综合运用
专题：
分析：根据提公因式法，可得平方差公式，再根据平方差公式，可分解因式．
解答：解：原式=（x-y）3[（x-y）2-1]
=（x-y）3（x-y+1）（x-y-1）．
=（x-y）3（x-y+1）（x-y-1）．
点评：本题考查了因式分解，把（x-y）3看作公因式是解题关键．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
如图，长方形内有两个面积分别为5，2的正方形，求阴影部分的面积．
如图，已知DE∥AB，FE∥DB，BD平分∠ABC．求证：EF平分∠CED．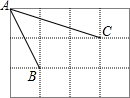
如图，在正方形网格中，小正方形的边长均为1，点A、B、C都是格点，则cos∠BAC=方程（x+1）（x-2）=x-2的解为（ ）
| A、x=0 |
| B、x=-1 |
| C、x1=2，x2=-1 |
| D、x1=0，x2=2 |