题目内容
13.计算:(1)($\sqrt{3}$)3-(3+2$\sqrt{3}$)÷$\sqrt{3}$
(2)($\sqrt{3}$+2)2×($\sqrt{3}$-2)2+3${\;}^{\frac{1}{2}}$×9${\;}^{-\frac{1}{4}}$.
分析 (1)根据二次根式的乘除法则运算;
(2)根据平方差公式和同底数幂的乘法法则运算.
解答 解:(1)原式=3$\sqrt{3}$-$\sqrt{3}$-2
=2$\sqrt{3}$-2;
(2)原式=[($\sqrt{3}$+2)($\sqrt{3}$-2)]2+${3}^{\frac{1}{2}}$•${3}^{-2×\frac{1}{4}}$
=(3-4)2+${3}^{\frac{1}{2}-\frac{1}{2}}$
=1+1
=2.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
3.一次函数y=x+2的图象与x轴交点的坐标是( )
| A. | (0,2) | B. | (0,-2) | C. | (2,0) | D. | (-2,0) |
4.观察下表规律,
利用规律如果$\root{3}{2.37}$=1.333,$\root{3}{23.7}$=2.872,则$\root{3}{0.0237}$=0.2872.
| a | 0.008 | 8 | 8000 | 8000000 |
| $\root{3}{a}$ | 0.2 | 2 | 20 | 200 |
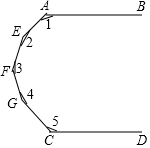 如图,AB∥CD,则∠1+∠2+∠3+∠4+∠5=720°.
如图,AB∥CD,则∠1+∠2+∠3+∠4+∠5=720°.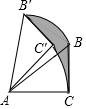 如图,在△ABC中,∠ACB=90°,BC=5,将△ABC绕顶点A按逆时针方向旋转45°至△AB′C′的位置,则线段BC扫过的区域(图中阴影部分)面积为$\frac{25π}{8}$.
如图,在△ABC中,∠ACB=90°,BC=5,将△ABC绕顶点A按逆时针方向旋转45°至△AB′C′的位置,则线段BC扫过的区域(图中阴影部分)面积为$\frac{25π}{8}$.