题目内容
8.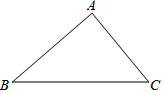 已知,如图,在△ABC中,∠B=45°,∠C=60°,AB=3$\sqrt{2}$.
已知,如图,在△ABC中,∠B=45°,∠C=60°,AB=3$\sqrt{2}$.(1)∠A=75°;
(2)求点A到BC的距离;
(3)求BC的长(结果用根号表示)
分析 (1)根据三角形内角和定理计算即可;
(2)根据正弦的定义求出AD;
(3)根据正切的定义求出CD,计算即可.
解答 解:(1)∠A=180°-(∠B+∠C)=75°,
故答案为:75;
(2)作AD⊥BC于D,
在Rt△ABD中,AD=AB×sin∠B=3,
即点A到BC的距离为3;
(3)在Rt△ABD中,BD=AB×cos∠B=3,
在Rt△ACD中,CD=$\frac{AD}{tan∠C}$=$\sqrt{3}$,
则BC=BD+CD=3+$\sqrt{3}$.
点评 本题考查的是解直角三角形,掌握锐角三角函数的概念是解题的关键.

练习册系列答案
相关题目
16.如图,过点P画出直线AB的垂线.下列画法中,正确的是( )
| A. |  | B. |  | C. |  | D. |  |
3.一次函数y=x+2的图象与x轴交点的坐标是( )
| A. | (0,2) | B. | (0,-2) | C. | (2,0) | D. | (-2,0) |
 已知:如图,∠A=∠ADE,∠C=∠E.
已知:如图,∠A=∠ADE,∠C=∠E.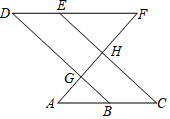 如图,点B、E分别在直线AC和DF上,若∠AGB=∠EHF,∠C=∠D,可以证明∠A=∠F.请完成下面证明过程中的各项“填空”.
如图,点B、E分别在直线AC和DF上,若∠AGB=∠EHF,∠C=∠D,可以证明∠A=∠F.请完成下面证明过程中的各项“填空”.