题目内容
7. 如图,四边形ABCD是正方形,E、F分别是AB、AD上的一点,且BF⊥CE,垂足为G,求证:AF=BE.
如图,四边形ABCD是正方形,E、F分别是AB、AD上的一点,且BF⊥CE,垂足为G,求证:AF=BE.
分析 直接利用已知得出∠BCE=∠ABF,进而利用全等三角形的判定与性质得出AF=BE.
解答 证明:∵四边形ABCD是正方形,
∴AB=BC,∠A=∠CBE=90°,
∵BF⊥CE,
∴∠BCE+∠CBG=90°,
∵∠ABF+∠CBG=90°,
∴∠BCE=∠ABF,
在△BCE和△ABF中
$\left\{\begin{array}{l}{∠BCE=∠ABF}\\{BC=AB}\\{∠CBE=∠A}\end{array}\right.$,
∴△BCE≌△ABF(ASA),
∴BE=AF.
点评 此题主要考查了正方形的性质以及全等三角形的判定与性质,正确得出△BCE≌△ABF是解题关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
15.2的相反数是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -2 |
12.PM2.5是指大气中直径小于或等于2.5μm(1μm=0.000001m)的颗粒物,也称为可入肺颗粒物,它们含有一定量的有毒、有害物质,对人体健康和大气环境质量有很大影响.2.3μm用科学记数法可表示为( )
| A. | 23×10-5m | B. | 2.3×10-5m | C. | 2.3×10-6m | D. | 0.23×10-7m |
19. 如图,在矩形AOBC中,O为坐标原点,OA、OB分别在x轴、y轴上,点B的坐标为(0,3$\sqrt{3}$),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为( )
如图,在矩形AOBC中,O为坐标原点,OA、OB分别在x轴、y轴上,点B的坐标为(0,3$\sqrt{3}$),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为( )
 如图,在矩形AOBC中,O为坐标原点,OA、OB分别在x轴、y轴上,点B的坐标为(0,3$\sqrt{3}$),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为( )
如图,在矩形AOBC中,O为坐标原点,OA、OB分别在x轴、y轴上,点B的坐标为(0,3$\sqrt{3}$),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为( )| A. | ($\frac{3}{2}$,$\frac{3}{2}\sqrt{3}$) | B. | (2,$\frac{3}{2}\sqrt{3}$) | C. | ($\frac{3}{2}\sqrt{3}$,$\frac{3}{2}$) | D. | ($\frac{3}{2}$,3-$\frac{3}{2}\sqrt{3}$) |
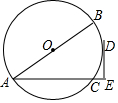 如图,已知⊙O的直径AB=12,弦AC=10,D是$\widehat{BC}$的中点,过点D作DE⊥AC,交AC的延长线于点E.
如图,已知⊙O的直径AB=12,弦AC=10,D是$\widehat{BC}$的中点,过点D作DE⊥AC,交AC的延长线于点E.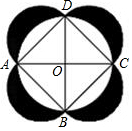 已知⊙O的两条直径AC,BD互相垂直,分别以AB,BC,CD,DA为直径向外作半圆得到如图所示的图形,现随机地向该图形内掷一枚小针,记针尖落在阴影区域内的概率为P1,针尖落在⊙O内的概率为P2,则$\frac{{P}_{1}}{{P}_{2}}$=$\frac{2}{π}$.
已知⊙O的两条直径AC,BD互相垂直,分别以AB,BC,CD,DA为直径向外作半圆得到如图所示的图形,现随机地向该图形内掷一枚小针,记针尖落在阴影区域内的概率为P1,针尖落在⊙O内的概率为P2,则$\frac{{P}_{1}}{{P}_{2}}$=$\frac{2}{π}$.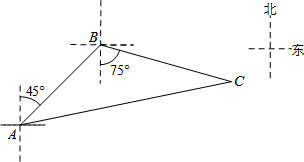 如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发行驶了2小时,在C处成功拦截捕鱼船,求捕鱼船的速度.
如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发行驶了2小时,在C处成功拦截捕鱼船,求捕鱼船的速度.