题目内容
18.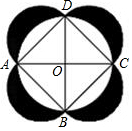 已知⊙O的两条直径AC,BD互相垂直,分别以AB,BC,CD,DA为直径向外作半圆得到如图所示的图形,现随机地向该图形内掷一枚小针,记针尖落在阴影区域内的概率为P1,针尖落在⊙O内的概率为P2,则$\frac{{P}_{1}}{{P}_{2}}$=$\frac{2}{π}$.
已知⊙O的两条直径AC,BD互相垂直,分别以AB,BC,CD,DA为直径向外作半圆得到如图所示的图形,现随机地向该图形内掷一枚小针,记针尖落在阴影区域内的概率为P1,针尖落在⊙O内的概率为P2,则$\frac{{P}_{1}}{{P}_{2}}$=$\frac{2}{π}$.
分析 直接利用圆的面积求法结合正方形的性质得出P1,P2的值即可得出答案.
解答 解:设⊙O的半径为1,则AD=$\sqrt{2}$,
故S圆O=π,
阴影部分面积为:π$(\frac{\sqrt{2}}{2})^{2}$×2+$\sqrt{2}$×$\sqrt{2}$-π=2,
则P1=$\frac{2}{π+2}$,P2=$\frac{π}{π+2}$,
故$\frac{{P}_{1}}{{P}_{2}}$=$\frac{2}{π}$.
故答案为:$\frac{2}{π}$.
点评 此题主要考查了几何概率,正确得出各部分面积是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.“五一”期间,某市共接待海内外游客约567000人次,将567000用科学记数法表示为( )
| A. | 567×103 | B. | 56.7×104 | C. | 5.67×105 | D. | 0.567×106 |
9.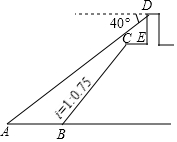 如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).
如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).
 如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).
如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).| A. | 5.1米 | B. | 6.3米 | C. | 7.1米 | D. | 9.2米 |
6.下列计算正确的是( )
| A. | a5+a5=a10 | B. | a7÷a=a6 | C. | a3•a2=a6 | D. | (-a3)2=-a6 |
3. 如图,函数y1=-2x与y2=ax+3的图象相交于点A(m,2),则关于x的不等式-2x>ax+3的解集是( )
如图,函数y1=-2x与y2=ax+3的图象相交于点A(m,2),则关于x的不等式-2x>ax+3的解集是( )
 如图,函数y1=-2x与y2=ax+3的图象相交于点A(m,2),则关于x的不等式-2x>ax+3的解集是( )
如图,函数y1=-2x与y2=ax+3的图象相交于点A(m,2),则关于x的不等式-2x>ax+3的解集是( )| A. | x>2 | B. | x<2 | C. | x>-1 | D. | x<-1 |
8.下面四个几何体:

其中,俯视图是四边形的几何体个数是( )

其中,俯视图是四边形的几何体个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 如图,E是?ABCD的边AD的中点,连接CE并延长交BA的延长线于F,若CD=6,求BF的长.
如图,E是?ABCD的边AD的中点,连接CE并延长交BA的延长线于F,若CD=6,求BF的长. 如图,四边形ABCD是正方形,E、F分别是AB、AD上的一点,且BF⊥CE,垂足为G,求证:AF=BE.
如图,四边形ABCD是正方形,E、F分别是AB、AD上的一点,且BF⊥CE,垂足为G,求证:AF=BE.