题目内容
19. 如图,在矩形AOBC中,O为坐标原点,OA、OB分别在x轴、y轴上,点B的坐标为(0,3$\sqrt{3}$),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为( )
如图,在矩形AOBC中,O为坐标原点,OA、OB分别在x轴、y轴上,点B的坐标为(0,3$\sqrt{3}$),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为( )| A. | ($\frac{3}{2}$,$\frac{3}{2}\sqrt{3}$) | B. | (2,$\frac{3}{2}\sqrt{3}$) | C. | ($\frac{3}{2}\sqrt{3}$,$\frac{3}{2}$) | D. | ($\frac{3}{2}$,3-$\frac{3}{2}\sqrt{3}$) |
分析 根据翻折变换的性质结合锐角三角函数关系得出对应线段长,进而得出D点坐标.
解答  解:∵四边形AOBC是矩形,∠ABO=30°,点B的坐标为(0,3$\sqrt{3}$),
解:∵四边形AOBC是矩形,∠ABO=30°,点B的坐标为(0,3$\sqrt{3}$),
∴AC=OB=3$\sqrt{3}$,∠CAB=30°,
∴BC=AC•tan30°=3$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=3,
∵将△ABC沿AB所在直线对折后,点C落在点D处,
∴∠BAD=30°,AD=3$\sqrt{3}$,
过点D作DM⊥x轴于点M,
∵∠CAB=∠BAD=30°,
∴∠DAM=30°,
∴DM=$\frac{1}{2}$AD=$\frac{3\sqrt{3}}{2}$,
∴AM=3$\sqrt{3}$×cos30°=$\frac{9}{2}$,
∴MO=$\frac{9}{2}$-3=$\frac{3}{2}$,
∴点D的坐标为($\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$).
故选:A.
点评 此题主要考查了翻折变换以及矩形的性质和锐角三角函数关系,正确得出∠DAM=30°是解题关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
9.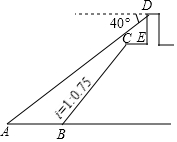 如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).
如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).
 如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).
如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).| A. | 5.1米 | B. | 6.3米 | C. | 7.1米 | D. | 9.2米 |
11.若x=-3,y=1,则代数式2x-3y+1的值为( )
| A. | -10 | B. | -8 | C. | 4 | D. | 10 |
8.下面四个几何体:

其中,俯视图是四边形的几何体个数是( )

其中,俯视图是四边形的几何体个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
6.某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.

根据以上信息解决下列问题:
(1)在统计表中,m=30,n=20,并补全条形统计图.
(2)扇形统计图中“C组”所对应的圆心角的度数是90°.
(3)若该校共有1120名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.
| 组别 | 正确字数x | 人数 |
| A | 0≤x<8 | 10 |
| B | 8≤x<16 | 15 |
| C | 16≤x<24 | 25 |
| D | 24≤x<32 | m |
| E | 32≤x<40 | n |

根据以上信息解决下列问题:
(1)在统计表中,m=30,n=20,并补全条形统计图.
(2)扇形统计图中“C组”所对应的圆心角的度数是90°.
(3)若该校共有1120名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.
 如图,E是?ABCD的边AD的中点,连接CE并延长交BA的延长线于F,若CD=6,求BF的长.
如图,E是?ABCD的边AD的中点,连接CE并延长交BA的延长线于F,若CD=6,求BF的长. 如图,四边形ABCD是正方形,E、F分别是AB、AD上的一点,且BF⊥CE,垂足为G,求证:AF=BE.
如图,四边形ABCD是正方形,E、F分别是AB、AD上的一点,且BF⊥CE,垂足为G,求证:AF=BE.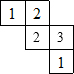 由一些大小相同的小正方体搭成的几何体的俯视图如图所示,其中正方形中的数字表示该位置上的小正方体的个数,那么该几何体的主视图是( )
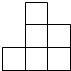
由一些大小相同的小正方体搭成的几何体的俯视图如图所示,其中正方形中的数字表示该位置上的小正方体的个数,那么该几何体的主视图是( )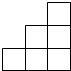

 如图,某人为了测量小山顶上的塔ED的高,他在山下的点A处测得塔尖点D的仰角为45°,再沿AC方向前进60m到达山脚点B,测得塔尖点D的仰角为60°,塔底点E的仰角为30°,求塔ED的高度.(结果保留根号)
如图,某人为了测量小山顶上的塔ED的高,他在山下的点A处测得塔尖点D的仰角为45°,再沿AC方向前进60m到达山脚点B,测得塔尖点D的仰角为60°,塔底点E的仰角为30°,求塔ED的高度.(结果保留根号)